Solve for part b

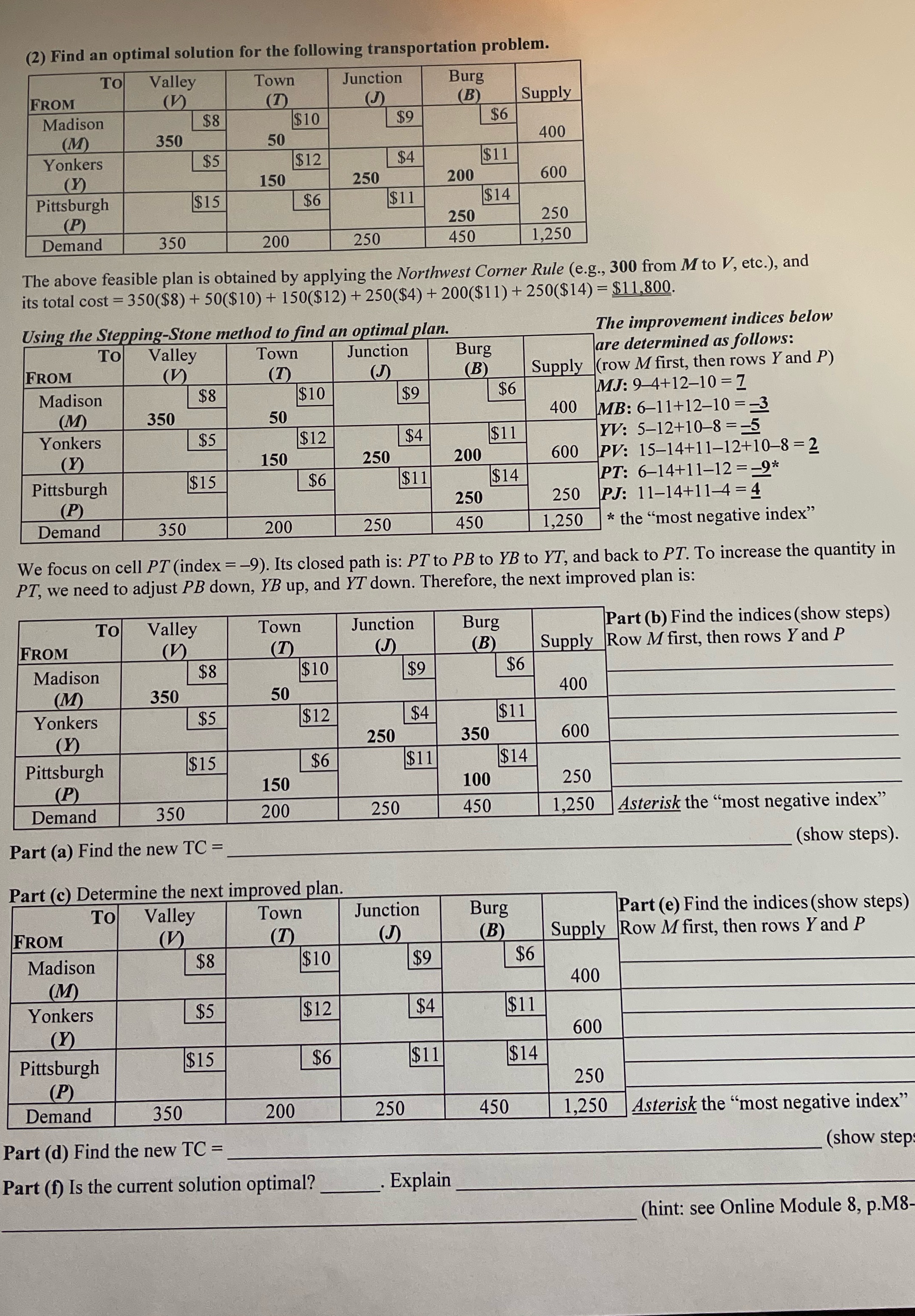
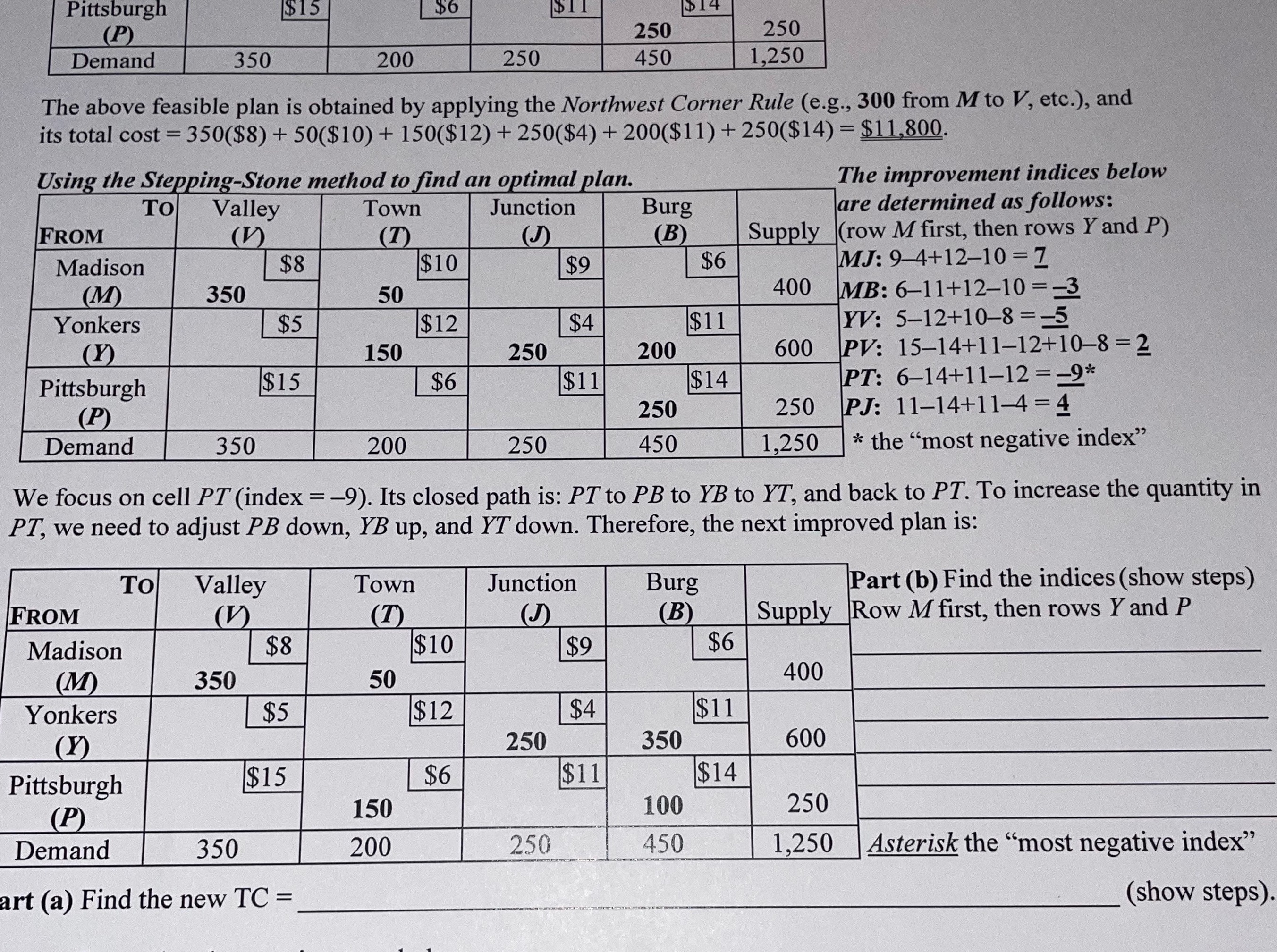
(2) Find an optimal solution for the following transportation problem. TO Valley Town Junction Burg FROM (V) (T) (B) Supply Madison $8 $10 $9 $6 (M) 350 50 400 Yonkers $5 $12 $4 $11 150 250 200 600 Pittsburgh $15 $6 $11 $14 (P) 250 250 Demand 350 200 250 450 1,250 The above feasible plan is obtained by applying the Northwest Corner Rule (e.g., 300 from M to V, etc.), and its total cost = 350($8) + 50($10) + 150($12) + 250($4) + 200($11) + 250($14) = $11,800. Using the Stepping-Stone method to find an optimal plan. The improvement indices below TO Valley Town Junction Burg are determined as follows: FROM (V) (T) (J) (B Supply (row M first, then rows Y and P) Madison $8 $10 $9 $6 MJ: 9 4+12-10 =Z (M) 350 50 400 MB: 6-11+12-10 = =3 Yonkers $5 $12 $4 $11 YV: 5-12+10-8 =-5 (Y) 150 250 600 PV: 15-14+11-12+10-8 =2 Pittsburgh $15 $6 $11 $14 PT: 6-14+11-12 =-9* (P) 250 250 PJ: 11-14+11-4 =4 Demand 350 200 250 450 1,250 * the "most negative index" We focus on cell PT (index = -9). Its closed path is: PT to PB to YB to YT, and back to PT. To increase the quantity in PT, we need to adjust PB down, YB up, and IT down. Therefore, the next improved plan is: TO Valley Town Junction Burg Part (b) Find the indices (show steps) FROM (V) (T) (J) (B Supply Row M first, then rows Y and P Madison $8 $10 $9 $6 (M) 350 50 400 Yonkers $5 $12 $4 $11 250 350 600 Pittsburgh $15 $6 $11 $14 (P) 150 100 250 Demand 350 200 250 450 1,250 Asterisk the "most negative index" Part (a) Find the new TC = (show steps). Part (c) Determine the next improved plan. TO Valley Town Junction Burg Part (e) Find the indices (show steps) FROM (V) (T) J (B Supply Row M first, then rows Y and P Madison $8 $10 $9 $6 (M) 400 Yonkers $5 $12 $4 $11 (Y) 600 Pittsburgh $15 $6 $11 $14 (P) 250 Demand 350 200 250 450 1,250 Asterisk the "most negative index" Part (d) Find the new TC = (show step Part (f) Is the current solution optimal? Explain hint: see Online Module 8, p.M8-Pittsburgh $15 $6 $ 14 P 250 250 Demand 350 200 250 450 1,250 The above feasible plan is obtained by applying the Northwest Corner Rule (e.g., 300 from M to V, etc.), and its total cost = 350($8) + 50($10) + 150($12) + 250($4) + 200($11) + 250($14) = $11,800. Using the Stepping-Stone method to find an optimal plan. The improvement indices below TO Valley Town Junction Burg are determined as follows: FROM (V) (T) (J) (B Supply (row M first, then rows Y and P) Madison $8 $10 $9 $6 MJ: 9-4+12-10 =Z (M) 350 50 400 MB: 6-11+12-10 = =3 Yonkers $5 $12 $4 $11 YV: 5-12+10-8 =-5 (Y 150 250 200 600 PV: 15-14+11-12+10-8 =2 Pittsburgh $15 $6 $11 $14 PT: 6-14+11-12 =-9* (P) 250 250 PJ: 11-14+11-4=4 Demand 350 200 250 450 1,250 * the "most negative index" We focus on cell PT (index = -9). Its closed path is: PT to PB to YB to YT, and back to PT. To increase the quantity in PT, we need to adjust PB down, YB up, and YT down. Therefore, the next improved plan is: To Valley Town Junction Burg Part (b) Find the indices (show steps) FROM (V) (T) J) B Supply Row M first, then rows Y and P Madison $8 $10 $9 $6 (M) 350 50 400 Yonkers $5 $12 $4 $11 (Y) 250 350 600 Pittsburgh $15 $6 $11 $14 (P) 150 100 250 Demand 350 200 250 450 1,250 Asterisk the "most negative index" art (a) Find the new TC = (show steps)