SOLVE IN PYTHON!!!

DON'T SOLVE IN MATLAB

DON'T SOLVE IT IF YOU ALREADY SOLVED THIS QUESTION, BEACUASE YOU ARE WRONG

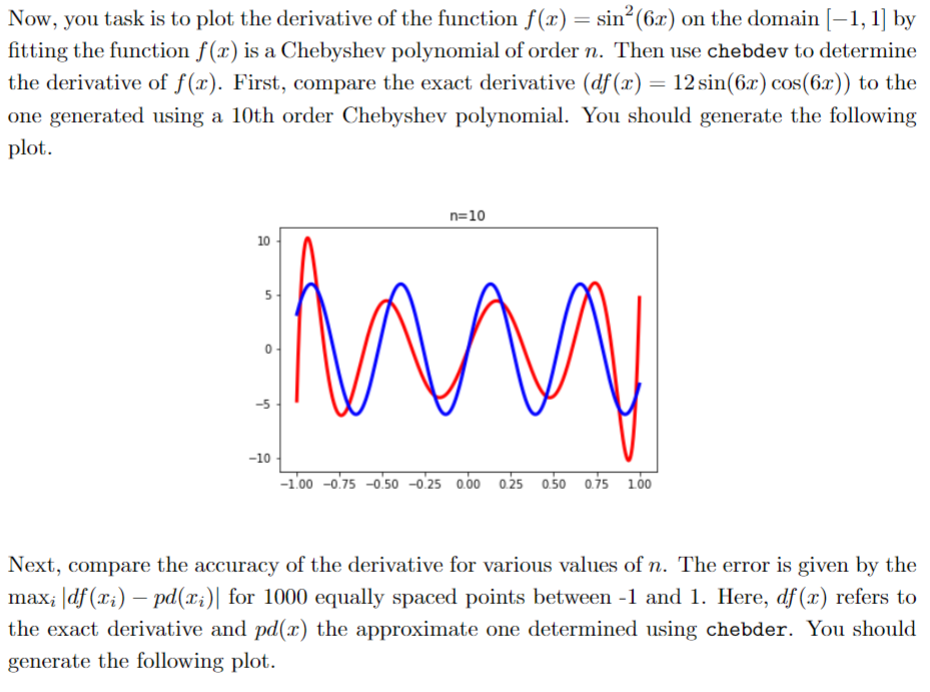
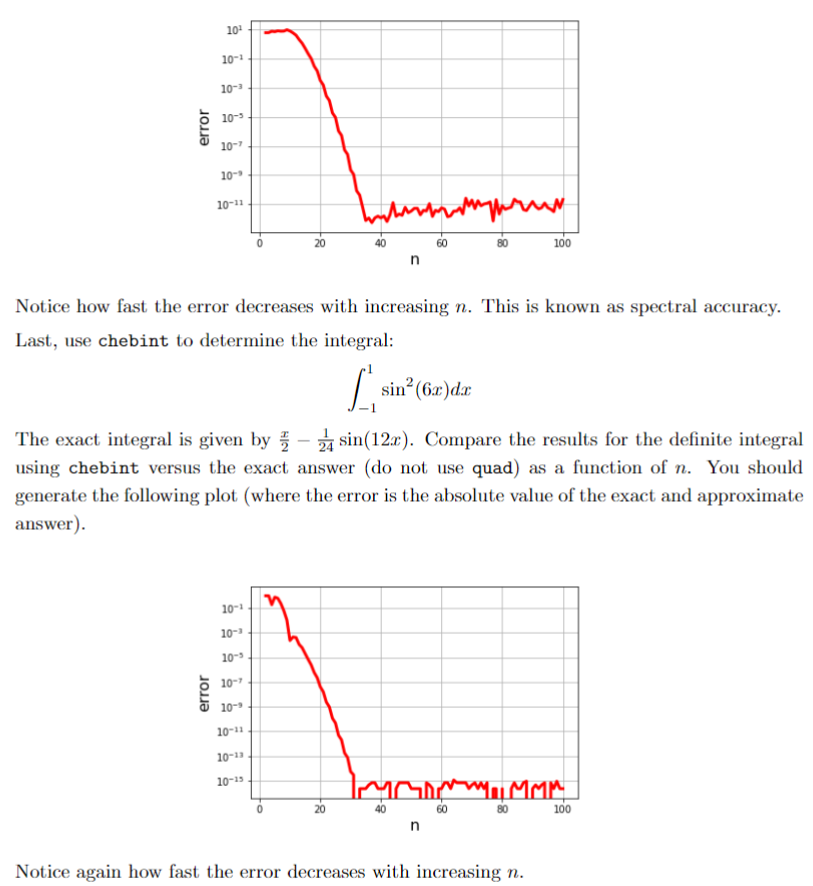
Now, you task is to plot the derivative of the function f(x)=sin2(6x) on the domain [1,1] by fitting the function f(x) is a Chebyshev polynomial of order n. Then use chebdev to determine the derivative of f(x). First, compare the exact derivative (df(x)=12sin(6x)cos(6x)) to the one generated using a 10th order Chebyshev polynomial. You should generate the following plot. Next, compare the accuracy of the derivative for various values of n. The error is given by the maxidf(xi)pd(xi) for 1000 equally spaced points between -1 and 1 . Here, df(x) refers to the exact derivative and pd(x) the approximate one determined using chebder. You should generate the following plot. Notice how fast the error decreases with increasing n. This is known as spectral accuracy. Last, use chebint to determine the integral: 11sin2(6x)dx The exact integral is given by 2x241sin(12x). Compare the results for the definite integra using chebint versus the exact answer (do not use quad) as a function of n. You shoul generate the following plot (where the error is the absolute value of the exact and approximate answer). Notice again how fast the error decreases with increasing n