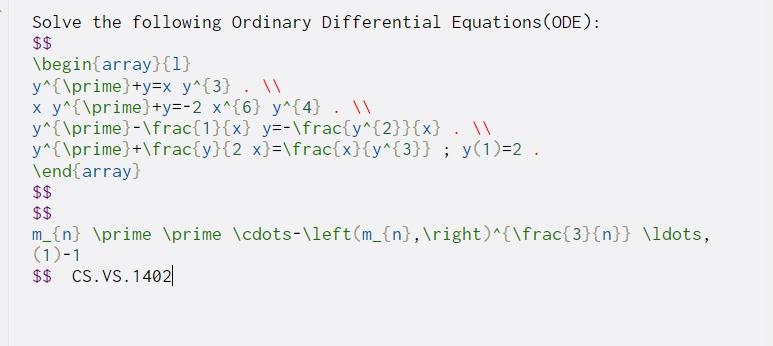
Solve the following Ordinary Differential Equations (ODE): $$ \begin{array}{1} y^{\prime} +y=x y^{3}. W x y^{\prime}+y=-2 X^{6} y^{4}. W y^{\prime}-\frac{1}{x} y=-\frac{y^{2}}{x} .W y^{\prime}+\frac{y}{2 x)=\frac{x}{y^{3}} ; y(1)=2 . \end{array} $$ $$ m_{n} \prime \prime \cdots-\left(m_{n}, ight)^{\frac{3}{n}} \ldots, (1)-1 $$ CS.VS. 14021