solve these question manually please

course :numirical mathod

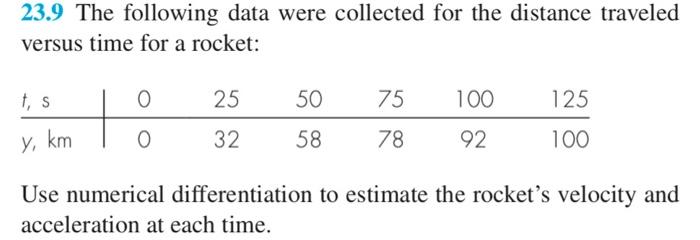
23.1 Compute forward and backward difference approximations of O(h) and O(h2), and central difference approximations of O(h2) and O(h4) for the first derivative of y=cosx at x=/4 using a value of h=/12. Estimate the true percent relative error t for each approximation. 23.3 Use centered difference approximations to estimate the first and second derivatives of y=ex at x=2 for h=0.1. Employ both O(h2) and O(h4) formulas for your estimates. 23.4 Use Richardson extrapolation to estimate the first derivative of y=cosx at x=/4 using step sizes of h1=/3 and h2=/6. Employ centered differences of O(h2) for the initial estimates. 23.9 The following data were collected for the distance traveled versus time for a rocket: Use numerical differentiation to estimate the rocket's velocity and acceleration at each time