Solve using Dijkstra's algorithm

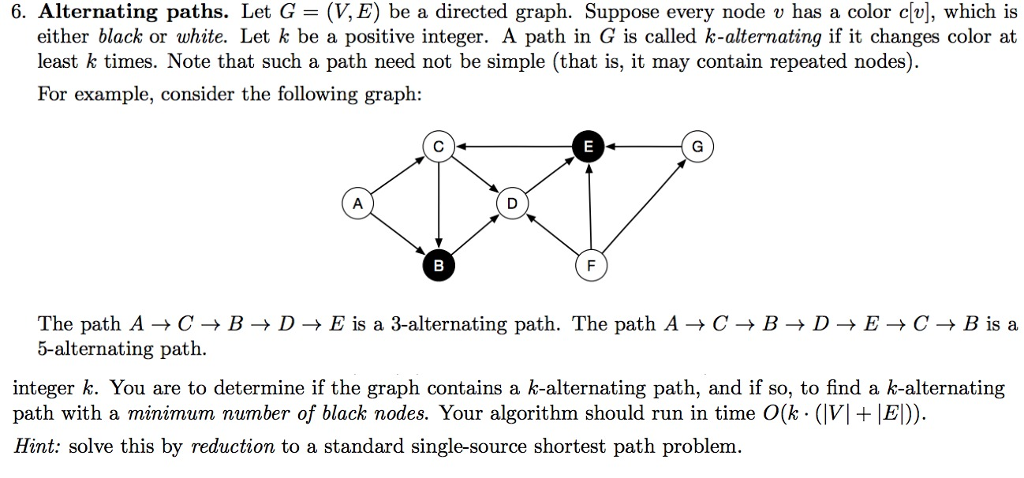
6. Alternating paths. Let G = (V,E) be a directed graph. Suppose every node v has a color c[u], which is either black or white. Let k be a positive integer. A path in G is called k-alternating if it changes color at least k times. Note that such a path need not be simple (that is, it may contain repeated nodes). For example, consider the following graph: The path A-+ C-> B-> D-> E is a 3-alternating path. The path A-> C-> B-+ D-+ E-+ C-+ B is a 5-alternating path. integer k. You are to determine if the graph contains a k-alternating path, and if so, to find a k-alternating path with a minimum number of black nodes. Your algorithm should run in time 0(k-(M + ). Hint: solve this by reduction to a standard single-source shortest path problem 6. Alternating paths. Let G = (V,E) be a directed graph. Suppose every node v has a color c[u], which is either black or white. Let k be a positive integer. A path in G is called k-alternating if it changes color at least k times. Note that such a path need not be simple (that is, it may contain repeated nodes). For example, consider the following graph: The path A-+ C-> B-> D-> E is a 3-alternating path. The path A-> C-> B-+ D-+ E-+ C-+ B is a 5-alternating path. integer k. You are to determine if the graph contains a k-alternating path, and if so, to find a k-alternating path with a minimum number of black nodes. Your algorithm should run in time 0(k-(M + ). Hint: solve this by reduction to a standard single-source shortest path