solve using modified given functions

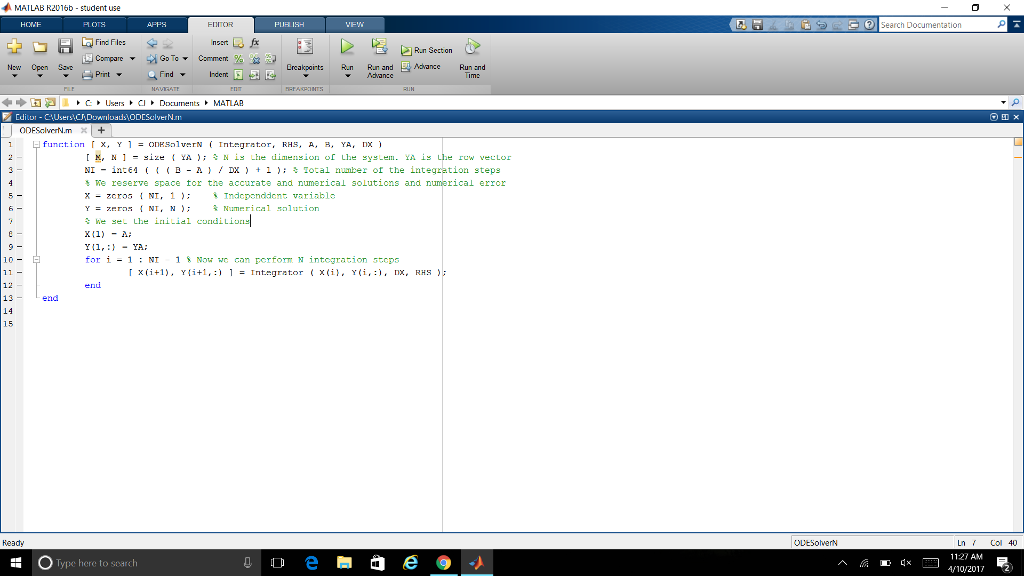
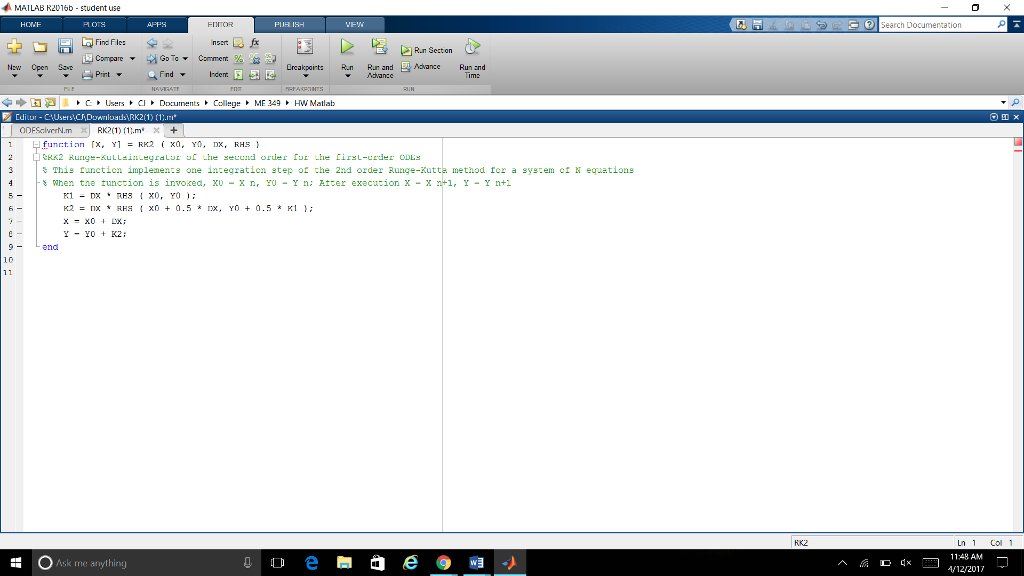
MATLAB files-2017 2017-5pring-ME319-Ho C Secure I ualearn.blackboard.com/ dt-content-rid-23320326 1/courses/15232 ME349-Homework https pdf 2. Plot the obtained numerical solution. Problem 2. Solve corrected problem 32 on page 319 of Gilat's book using the function ODESolver1 with the RK2 method and the integration step size At 0.01 32. A water tank shaped as an ellipsoid a 1.5 m, b 4.0 m, c 3m) has a circular hole at the bot tom, as shown. According to Torricelli's law, the speed v of the water that is discharging from the hole is given by gh where h is the height of the water and g 9.81m/ s2. The rate at which the height, h, of the water in the tank changes as the water flows out through the hole is given by r 0.025m. 2ghr dt (h ab 1 where r is the radius of the hole. Solve the differential equation for h The initial height of the water is h(0) 5.9 m. Solve the problem for different times and find an estimate for the time when h(t) 0.1 m. Make a plot of h as a function of time. a e Ask me any D 4x 247 AM MATLAB files-2017 2017-5pring-ME319-Ho C Secure I ualearn.blackboard.com/ dt-content-rid-23320326 1/courses/15232 ME349-Homework https pdf 2. Plot the obtained numerical solution. Problem 2. Solve corrected problem 32 on page 319 of Gilat's book using the function ODESolver1 with the RK2 method and the integration step size At 0.01 32. A water tank shaped as an ellipsoid a 1.5 m, b 4.0 m, c 3m) has a circular hole at the bot tom, as shown. According to Torricelli's law, the speed v of the water that is discharging from the hole is given by gh where h is the height of the water and g 9.81m/ s2. The rate at which the height, h, of the water in the tank changes as the water flows out through the hole is given by r 0.025m. 2ghr dt (h ab 1 where r is the radius of the hole. Solve the differential equation for h The initial height of the water is h(0) 5.9 m. Solve the problem for different times and find an estimate for the time when h(t) 0.1 m. Make a plot of h as a function of time. a e Ask me any D 4x 247 AM