SOLVE USING PYTHON, DO NOT ANSWER WITH MATLAB CODE. PYTHON ONLY. ANSWER WILL BE DOWN VOTED IF NOT SOLVED IN PYTHON.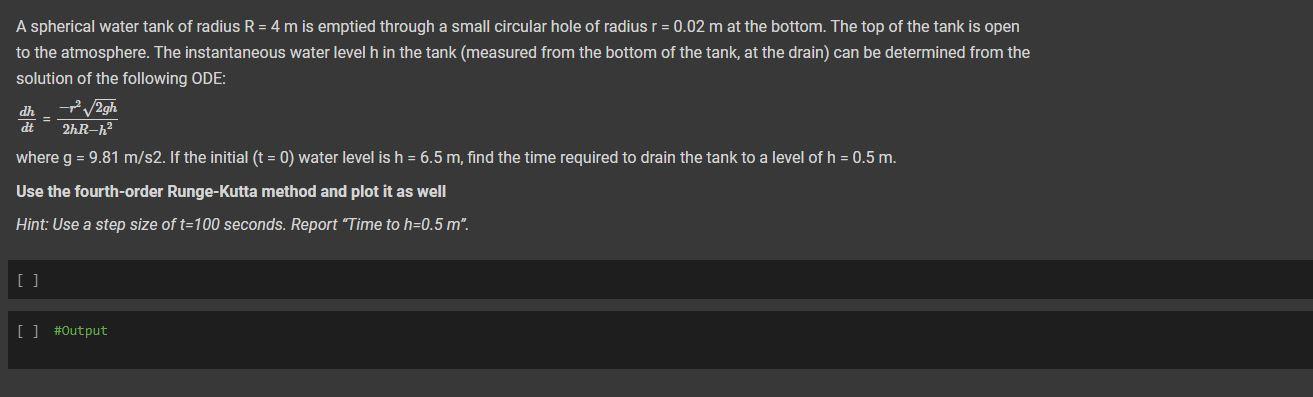

A spherical water tank of radius R = 4 m is emptied through a small circular hole of radius r = 0.02 m at the bottom. The top of the tank is open to the atmosphere. The instantaneous water level h in the tank (measured from the bottom of the tank, at the drain) can be determined from the solution of the following ODE: dh - 2gh dt 2hR-h? where g = 9.81 m/s2. If the initial (t = 0) water level is h = 6.5 m, find the time required to drain the tank to a level of h = 0.5 m. Use the fourth-order Runge-Kutta method and plot it as well Hint: Use a step size of t=100 seconds. Report Time to h=0.5 m". [] [] #Output