SOLVE WITH MATLAB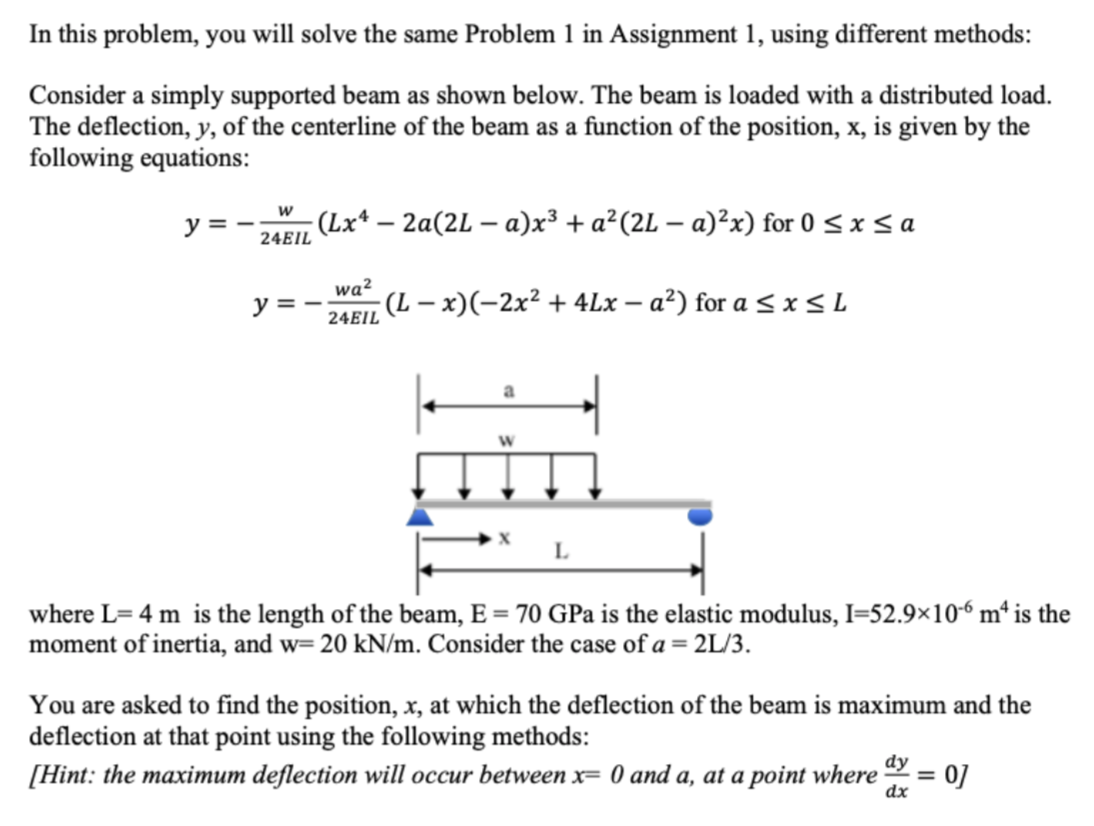

In this problem, you will solve the same Problem 1 in Assignment 1, using different methods: Consider a simply supported beam as shown below. The beam is loaded with a distributed load. The deflection, y, of the centerline of the beam as a function of the position, x, is given by the following equations: w y = (Lx4 2a(2L a)x3 + a(2L a)x) for 0 sx sa 24EIL y=- wa2 (L - x)(-2x2 + 4Lx a?) for a sxsL 24EIL w L where L=4 m is the length of the beam, E = 70 GPa is the elastic modulus, 1=52.9x10-6 m^ is the moment of inertia, and w= 20 kN/m. Consider the case of a = 2L/3. You are asked to find the position, x, at which the deflection of the beam is maximum and the deflection at that point using the following methods: [Hint: the maximum deflection will occur between x= 0 and a, at a point where ax = 0] Write a MATLAB function that implements the Newton's method to solve f(x)=0, with following inputs and outputs: Inputs: initial guess, maximum iterations, tolerance, and the name (string) of the m-file that returns f(x). Output: root of equation f(x)=0 obtained using Newton's method. Use your completed code to solve the problem and report the position, x, at which the deflection of the beam is maximum and the deflection at that point. Also include your code in your submission. In this problem, you will solve the same Problem 1 in Assignment 1, using different methods: Consider a simply supported beam as shown below. The beam is loaded with a distributed load. The deflection, y, of the centerline of the beam as a function of the position, x, is given by the following equations: w y = (Lx4 2a(2L a)x3 + a(2L a)x) for 0 sx sa 24EIL y=- wa2 (L - x)(-2x2 + 4Lx a?) for a sxsL 24EIL w L where L=4 m is the length of the beam, E = 70 GPa is the elastic modulus, 1=52.9x10-6 m^ is the moment of inertia, and w= 20 kN/m. Consider the case of a = 2L/3. You are asked to find the position, x, at which the deflection of the beam is maximum and the deflection at that point using the following methods: [Hint: the maximum deflection will occur between x= 0 and a, at a point where ax = 0] Write a MATLAB function that implements the Newton's method to solve f(x)=0, with following inputs and outputs: Inputs: initial guess, maximum iterations, tolerance, and the name (string) of the m-file that returns f(x). Output: root of equation f(x)=0 obtained using Newton's method. Use your completed code to solve the problem and report the position, x, at which the deflection of the beam is maximum and the deflection at that point. Also include your code in your submission