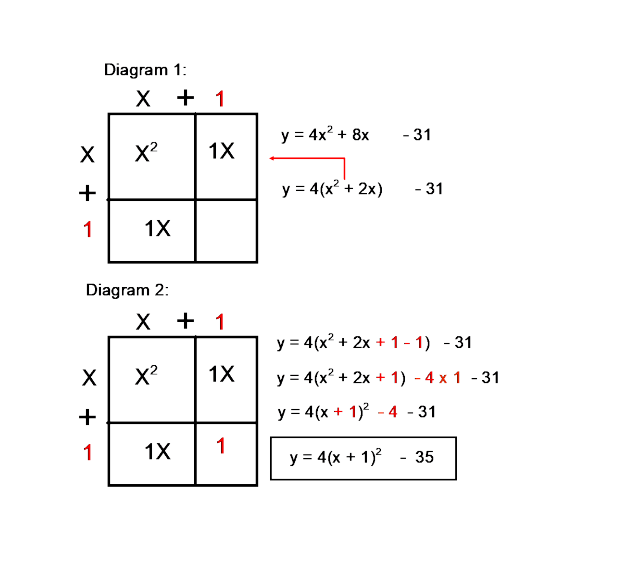
Solving Quadratics Visually by Using Al-Khwarizmi's Method Extended Objective To understand how to solve quadratics visually by using Al-Khwarizmi's method extended. Background Who is Al-Khwarizmi? He is pictured below left and is considered the "father" of algebra. He lived in Persia from about 780 to 850 CE. (CE means Common Era, and we used to write these dates as 850 AD). Example 1: Now the picture on the right below, is a problem with a solution attached. The puzzle translated into modern algebra would read: Solve: x2 + 10x = 39. So "x" is actually "its roots". What must be the square which, when increased by ten of its own roots, amounts to 39? Solution: You halve the number of roots, which in this Muhammad ibn case yields five. This you multiply by itself; Musa al-Khwarizmi the product is twenty-five. Add this to (c. 780-850) thirty-nine; the sum is sixty-four. Now take the root of this which is eight, and subtract from it half the number of roots, which is five; the remainder is three. This is the root of the square which you sought.Step 1: Write the equation out with a gap in it as seen on the left. x2 + 10x = 39 x2 + 10x = 39 X + X x2 5x + 5x X + 5 X 5x + 5x X +5 x2 + 10x + 25 = 39 + 25 x2 5x (x + 5)