someone pls help me

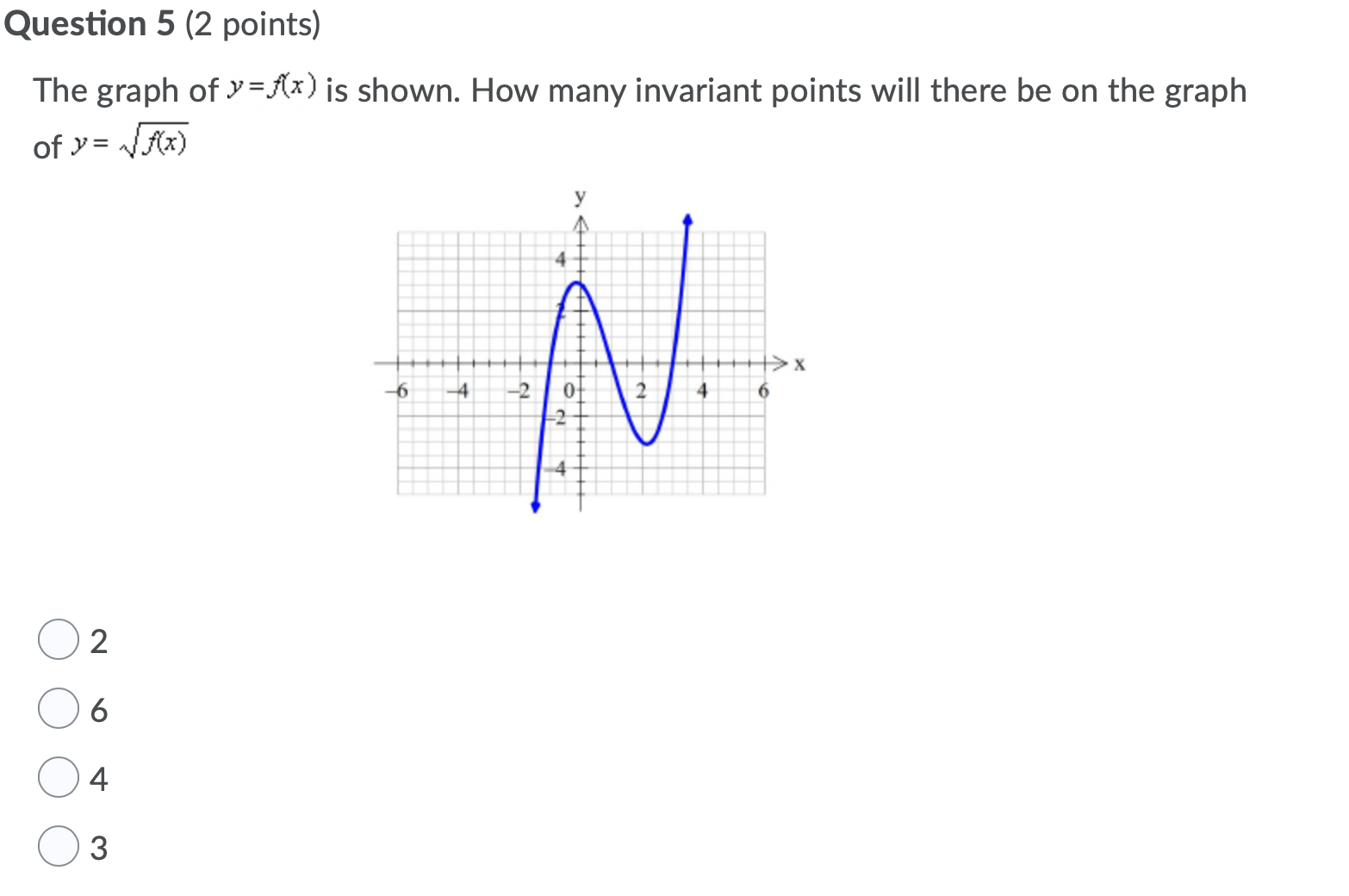
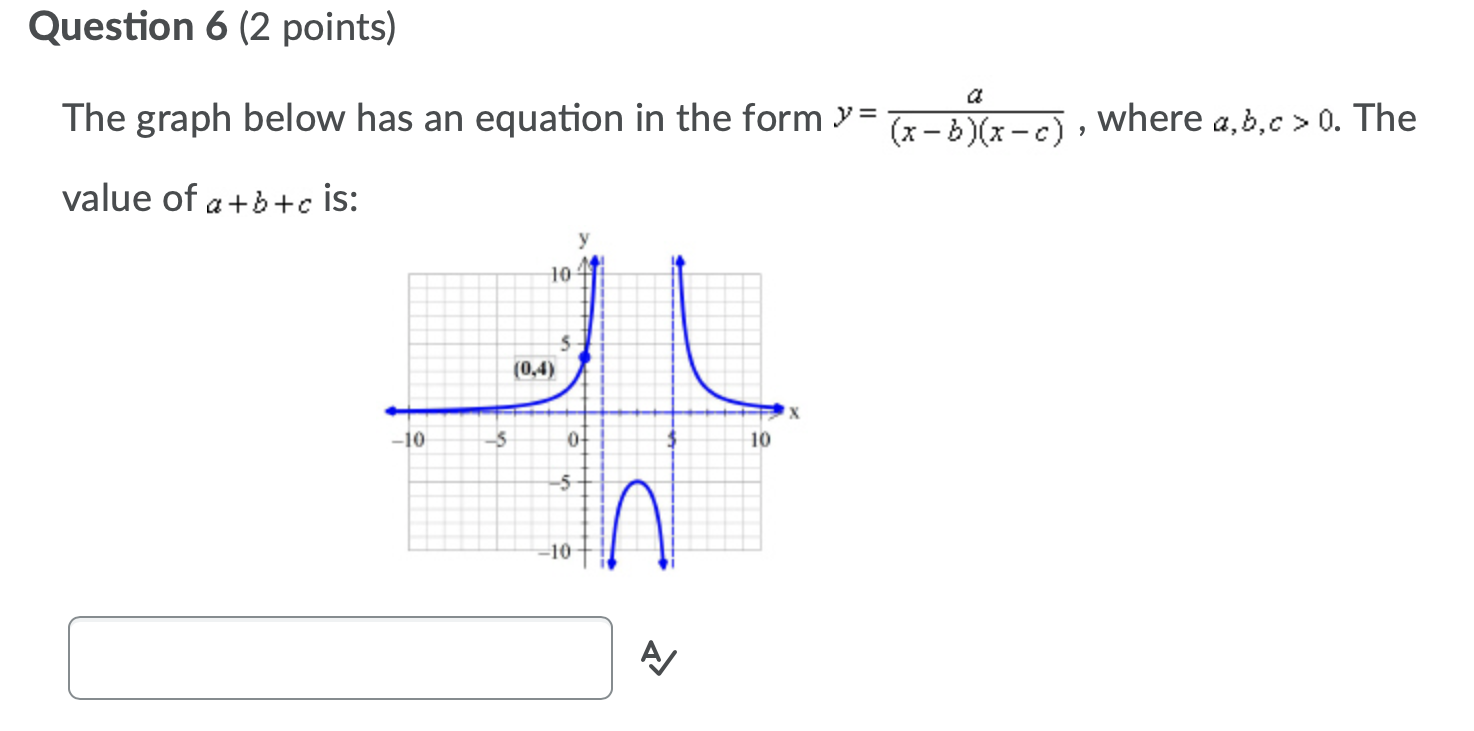
Given the graph below, the domain of the inverse is: 10 [0,5] (-00, 00) [-5,5] [0,00) Question 2 (2 points) A function p(x) = (x + 2)(x -4)(x - 3), is transformed to y= p -5 x . The possible new zeros of the function are listed below: Possible Zeros Zero #1: (1,0) Zero #2: (4,0) Zero #3: (-6,0) Zero #4: (-2,0) The Zero #5: (8,0) Zero #6: (-1,0) Zero #7: (-8,0) Zero #8: (-,0) new zeros of the transformed function are numbered: Enter your answer in increasing numerical order with no spaces or commasQuestion 3 (2 points) The equation which represents the graph of the inverse of y= x +4 is: Oy= (x - 4)2 , x >0 Oy=x2 - 16, x > 0 ( y = x+ 4, x >0 Oy= x2 - 4, x >0Question 4 (2 points) Given the rational function A(x) = x - 4 2x- -x - jo, Which of the following statements are true: The graph has a vertical asymptote x = 5, no horizontal asymptote and a point of discontinuity at x = -2 The graph has vertical asymptotes * = 5 and x = -2 and has a horizontal asymptote y = 7 O The graph has vertical asymptotes x = 5 and x = 2 and has a horizontal asymptote y= 0 The graph has a vertical asymptote * = 5 , a horizontal asymptote = 5 and a point of discontinuity at x = -2Question 5 (2 points) The graph of y=x) is shown. How many invariant points will there be on the graph of J'= Jx) Question 6 (2 points) The graph below has an equation in the form y= m , where a,b,c > 0. The value of a+b+c is