Specification: The GCDRM circuit is specified below using its: $1.$ Pseudocode of the functions gcd$($a$,$b$)$ and replace$\_$matrix$($int mat$[8][8])$ expressed using C$/$C$++$ notation. $2.$ Description of the operation of the main circuit. $3.$ Table of input$/$output ports.

$1.$ Pseudocode of the functions gcd$($a$,$b$)$ and replace$\_$matrix$($int mat$[8][8])$ expressed using C$/$C$++$ notation unsigned int gcd$($unsigned int a$,$ unsigned int b$)/*$ Function calculating greatest common divisor of a and b$,$ e$.$g$.,$ gcd$(42,70)=14*/\{/*$ Returning the result for the following special cases: gcd$(0,$ b$)==$ b; gcd$($a$,0)==$ a$,$ gcd$(0,0)==0*/$ if $($a $==0)$ return b; if $($b $==0)$ return a; $/*$ Finding k$,$ such that k is the greatest power of $2$ that divides both a and b $*/$ unsigned int k; for $($k $=0$; $(($a $|$ b$)$ & $1)==0$; $++$k$)\{$ a $>>=1$; b $>>=1$; $\}/*$ Dividing a by $2$ until a becomes odd $*/$ while $(($a & $1)==0)$ a $>>=1$; $/*$ From here on$,$ a is always odd $*/$ do $\{/*$ If b is even, remove all factors of $2$ in b $*/$ while $(($b & $1)==0)$ b $>>=1$; $/*$ Now a and b are both odd. Swap if necessary so a b$,$ then set b $=$ b $-$ a $($which is even$).*/2$ if $($a $>$ b$)$ swap$($a$,$ b$)$; b $=($b $-$ a$)$; $\}$ while $($b $!=0)$; $/*$ restore common factors of $2*/$ return a $$ k; $\}$ void replace$\_$matrix$($unsigned int mat$[8][8])\{$ unsigned int rgcd$[8]$; unsigned int cgcd$[8]$; $/*$ Initialize arrays of row and column gcds to zeros $*/$ for $($int i $=0$; i $<mtext></mtext><mn>8</mn>$; i$++)$ rgcd$[$i$]=0$; for $($int i $=0$; i $<mtext></mtext><mn>8</mn>$; i$++)$ cgcd$[$i$]=0$; $/*$ Calculate gcd of each row and each column in the array mat$[8][8]*/$ for $($int i $=0$; i $<mtext></mtext><mn>8</mn>$; i$++)\{$ for $($int j $=0$; j $<mtext></mtext><mn>8</mn>$; j$++)\{$ rgcd$[$i$]=$ gcd$($rgcd$[$i$],$ mat$[$i$][$j$])$; cgcd$[$j$]=$ gcd$($cgcd$[$j$],$ mat$[$i$][$j$])$; $\}\}/*$ Replace matrix element mat$[$i$][$j$]$ by the product of the gcds for the row i and column j $*/$ for $($int i $=0$; i $<mtext></mtext><mn>8</mn>$; i$++)$ for $($int j $=0$; j $<mtext></mtext><mn>8</mn>$; j$++)$ mat$[$i$][$j$]=$ rgcd$[$i$]*$ cgcd$[$j$]$; $\}$

$2.$ Description of the operation of the main circuit The GCDRM main circuit contains RAM capable of storing the array mat$[8][8],$ including $6432-$bit unsigned integers. When input s $==0,$ the GCDRM unit is fully controlled by an external circuit. When input s $==1,$ the GCDRM unit is controlled by its internal controller. As soon as s becomes $1,$ the GCDRM circuit executes the function replace$\_$matrix$($int mat$[8][8]),$ and then asserts done $=1.$ The external circuit performs the following sequence of operations in an infinite loop: $1.$ Setting input s to $0.2.$ Initializing mat$[8][8])$ using inputs din, x$,$ y$,$ we$,$ clk$.3.$ Setting s to $1$ and waiting for output done $=1.4.$ Setting input s to $0.5.$ Reading mat$[8][8])$ using inputs x$,$ y$,$ rd$,$ clk$,$ and output dout. $6.$ Go to step $2.$

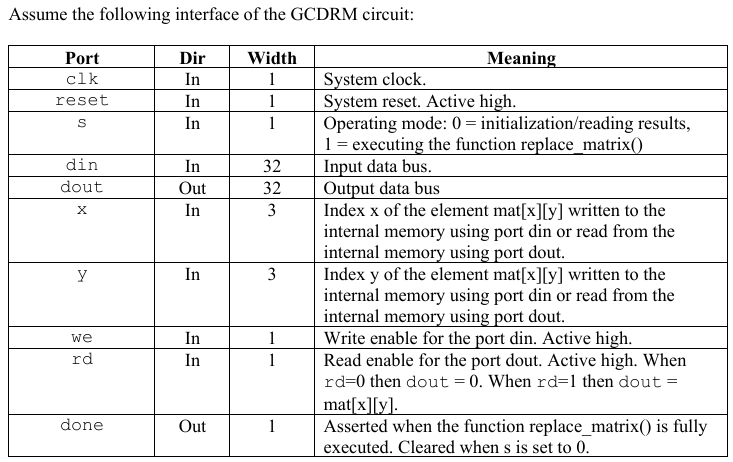
Assume the following interface of the GCDRM circuit: $($Attached image$)$

Task $1$ Draw a hierarchical block diagram of the Datapath of the GCDRM circuit. Assume Primary performance target: Minimum execution time. Secondary performance target: Minimum resource utilization. Minimize the number of control signals to be generated by the Control Unit. Please clearly mark the widths of all buses in your circuit. Use only well$-$known medium complexity combinational and sequential circuit building blocks. Clearly specify $$ names, widths and directions of all buses $$ names, widths and directions of all inputs and outputs of the logic components.

Task $2$ Draw an interface of the GCDRM circuit with the division into the Datapath and Controller.

Task $3$ Identify the most likely critical path in your circuit and mark it in your block diagram.