Question: Specifications for a part for a 3-D printer state that the part should weigh between 24 and 25 ounces. The process that produces the parts
- Specifications for a part for a 3-D printer state that the part should weigh between 24 and 25 ounces. The process that produces the parts has a mean of 24.5 ounces and a standard deviation of .2 ounce. The distribution of output is normal.
- What percentage of parts will not meet the weight specs?
- Within what values will 95.44 percent of the sample means of this process fall if samples of
n = 16 are taken and the process is in control (random)?
- Using the control limits from part b, would the following sample means be in control? 24.52,
24.53, 24.44, 24.51, 24.41, 24.39
- An automatic filling machine is used to fill 1-liter bottles of cola. The machines output is approxi- mately normal with a mean of 1.0 liter and a standard deviation of .01 liter. Output is monitored using means of samples of 25 observations.
- Determine upper and lower control limits that will include roughly 97 percent of the sample means when the process is in control.
- Given the following sample means1.005, 1.001, .998, 1.002, .995, and .999is the process in control?
- Is the process in control given the following sample means1.003, .999, .997, 1.001, 1.002, .998, and 1.004?
-
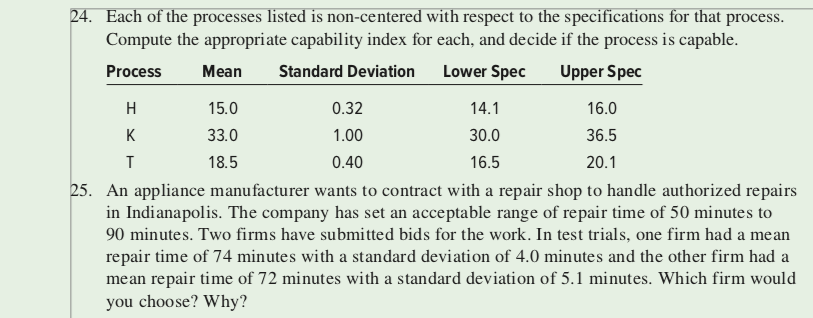
An appliance manufacturer wants to contract with a repair shop to handle authorized repairs in Indianapolis. The company has set an acceptable range of repair time of 50 minutes to 90 minutes. Two firms have submitted bids for the work. In test trials, one firm had a mean repair time of 74 minutes with a standard deviation of 4.0 minutes and the other firm had a mean repair time of 72 minutes with a standard deviation of 5.1 minutes. Which firm would you choose? Why?

Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


