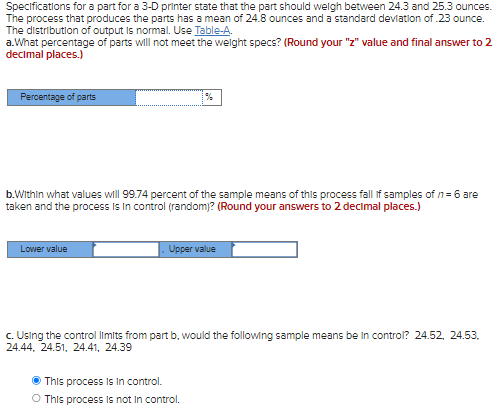
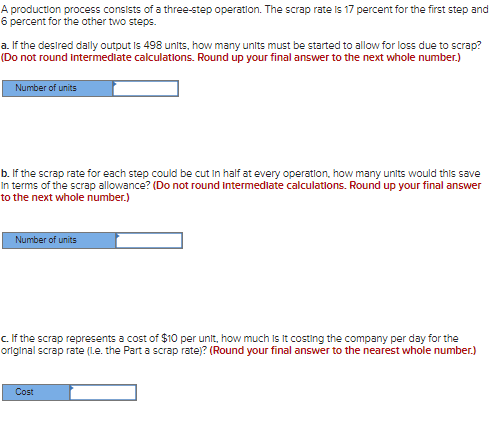
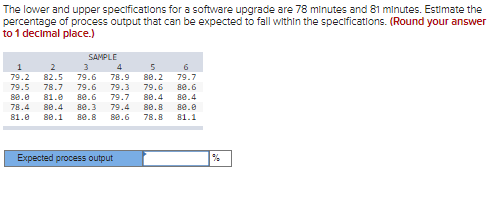
Speclfications for a part for a 3-D printer state that the part should weigh between 24.3 and 25.3 ounces. The process that produces the parts has a mean of 24.8 ounces and a standard devlation of 23 ounce. The distributlon of output is normal. Use Table-A. a.What percentage of parts will not meet the weight specs? (Round your " z " value and final answer to 2 decimal places.) b.Within what values will 99.74 percent of the sample means of this process fall if samples of n=6 are taken and the process is in control (random)? (Round your answers to 2 decimal places.) c. Using the control limits from part b, would the following sample means be in control? 24.52, 24.53, 24.44,24.51,24.41,24.39 This process is in control. This process is not in control. A production process consists of a three-step operation. The scrap rate is 17 percent for the first step and 6 percent for the other two steps. a. If the desired daily output is 498 units, how many units must be started to allow for loss due to scrap? (Do not round intermediate calculations. Round up your final answer to the next whole number.) b. If the scrap rate for each step could be cut in half at every operation, how many units would this save In terms of the scrap allowance? (Do not round intermedlate calculations. Round up your final answer to the next whole number.) c. If the scrap represents a cost of $10 per unit, how much is it costing the company per day for the original scrap rate (l.e. the Part a scrap rate)? (Round your final answer to the nearest whole number.) The lower and upper speclicatlons for a software upgrade are 78 minutes and 81 minutes. Estimate the percentage of process output that can be expected to fall within the specifications. (Round your answer to 1 decimal place.)