Spiral Horizontal Curve Problem:

Given:

$=27{13}^{\text{'}}{00}^{\text{'}\text{'}}$ Right

$D=2{00}^{\text{'}}($ convert $toR)$

$L_S=250ft.$

Sta. $\frac{?}{PI}=57+73\mathrm{.}92$

$N_{\frac{?}{PI}}=21,788\mathrm{.}57,E_{\frac{?}{PI}}=18,476\mathrm{.}32$

AZ of Back Tangent $=31{25}^{\text{'}}{15}^{\text{'}\text{'}}($tangent before curves$)$

Spiral at both ends of circular curve

Find:

Needed Circular and Spiral Curve Elements:

$R,{}_C,L,{}_S,x,Y,o,H$

Stationing for:

Sta. of TS$,$ SC$,$ CS$,$ ST

$3.$ Curve Layout Deflection Angles and Chords for:

Sta. $51+00\mathrm{.}00($on entrance spiral$)$

Sta. $58+00\mathrm{.}00($on circular curve$)$

Sta. $64+00\mathrm{.}00($on exit spiral$)$

$4.$ Coordinates $(N,E)$ for:

TS$,$ SC$,$ ST$,$

Sta. $51+00\mathrm{.}00,$

Sta. $58+00\mathrm{.}00,$

Sta. $64+00\mathrm{.}00$

$5.$ Draw a neat sketch showing all given and found elements.

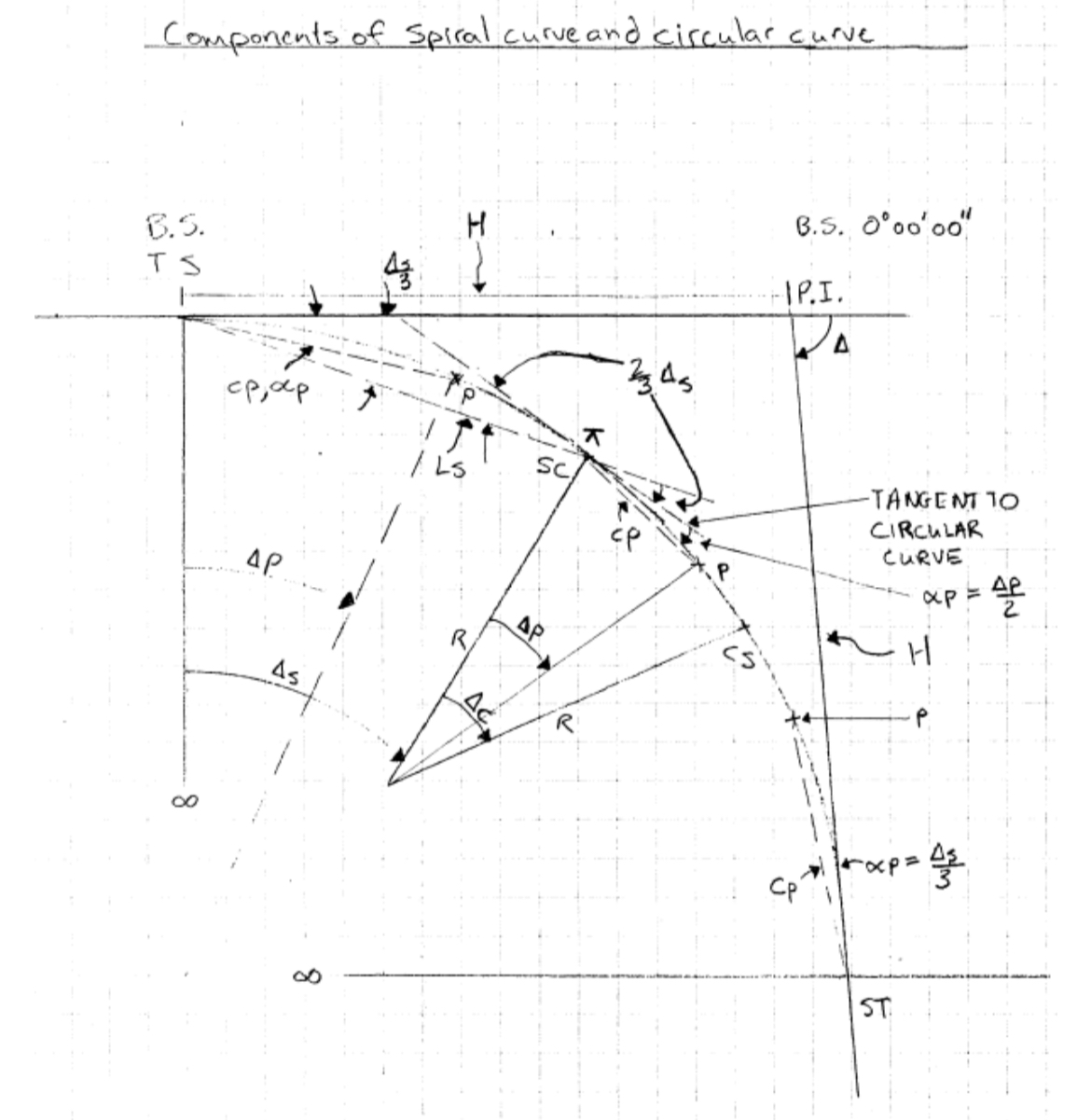
Spiral Curve Elements

Back Tangent AZ $=$

Point of Intersection, PI Sta. $=$

Deflection Angle at PI$,=$

Degree of Curve of Circular Curve, $D=$

Radius of Circular Curve, $R=$

Arc Length of Spiral, $L_S=$

Average Degree of Curve, D$/2=$

Spiral Angle, ${}_S=(\frac{L_S}{100})(\frac{D}{2})=$

Spiral Angle at Any Point, ${}_P=(\frac{L_P}{L_S}{)}^2{}_S$

Interior Circular Curve Angle, ${}_C=-2{}_S=$

X position of SC

$x=L_S(100-0\mathrm{.}0030462{}_s^2)(ft.),(L_{S}in$ stations $)$

$x=$

Y position of SC

Throw of Circular Curve

$o=Y-R(1-cos{}_S)$

$o=$

Tangent Length from TS to PI

$H=x-$Rsin${}_S+(R+o)tan(\frac{}{2})$

$H=$

Curve Stationing and Coordinates

A$.$ Preliminary PI Station

B$.$ Sta. TS $=$ Sta. PI $-H=$

C$.$ Sta. $SC=$Sta.$TS+L_S=$

D$.$ Sta. $CS=$Sta.$SC+L=$

E$.$ Sta.$ST=$Sta.$CS+L_S=$

Curve Layout by Deflection Angles and Chords

Deflection angle to any point P on spiral

${}_P=\frac{{}_P}{3},({}_P$ for spiral $)$

Chord to any point P on spiral

$c_P=L_P=$Sta.$P-$Sta.$TS$

Deflection angle to any point P on circular curve