Stable marriage problem: https://en.wikipedia.org/wiki/Stable_marriage_problem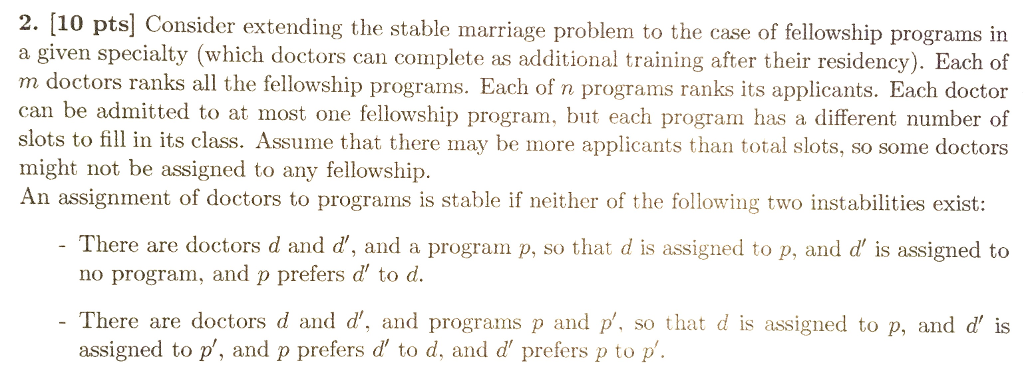

Consider extending the stable marriage problem to the case of fellowship programs in a given specialty (which doctors can complete as additional training after their residency). Each of m doctors ranks all the fellowship programs. Each of n programs ranks its applicants. Each doctor can be admitted to at most one fellowship program, but each program has a different number of slots to fill in its class. Assume that there may be more applicants than total slots, so some doctors might not be assigned to any fellowship. An assignment of doctors to programs is stable if neither of the following two instabilities exist: There are doctors d and d', and a program p, so that d is assigned to p, and d' is assigned to no program, and p prefers d' to d. There are doctors d and d', and programs p and p'. so that d is assigned to p, and d' is assigned to p', and p prefers d' to d, and d' prefers p to p