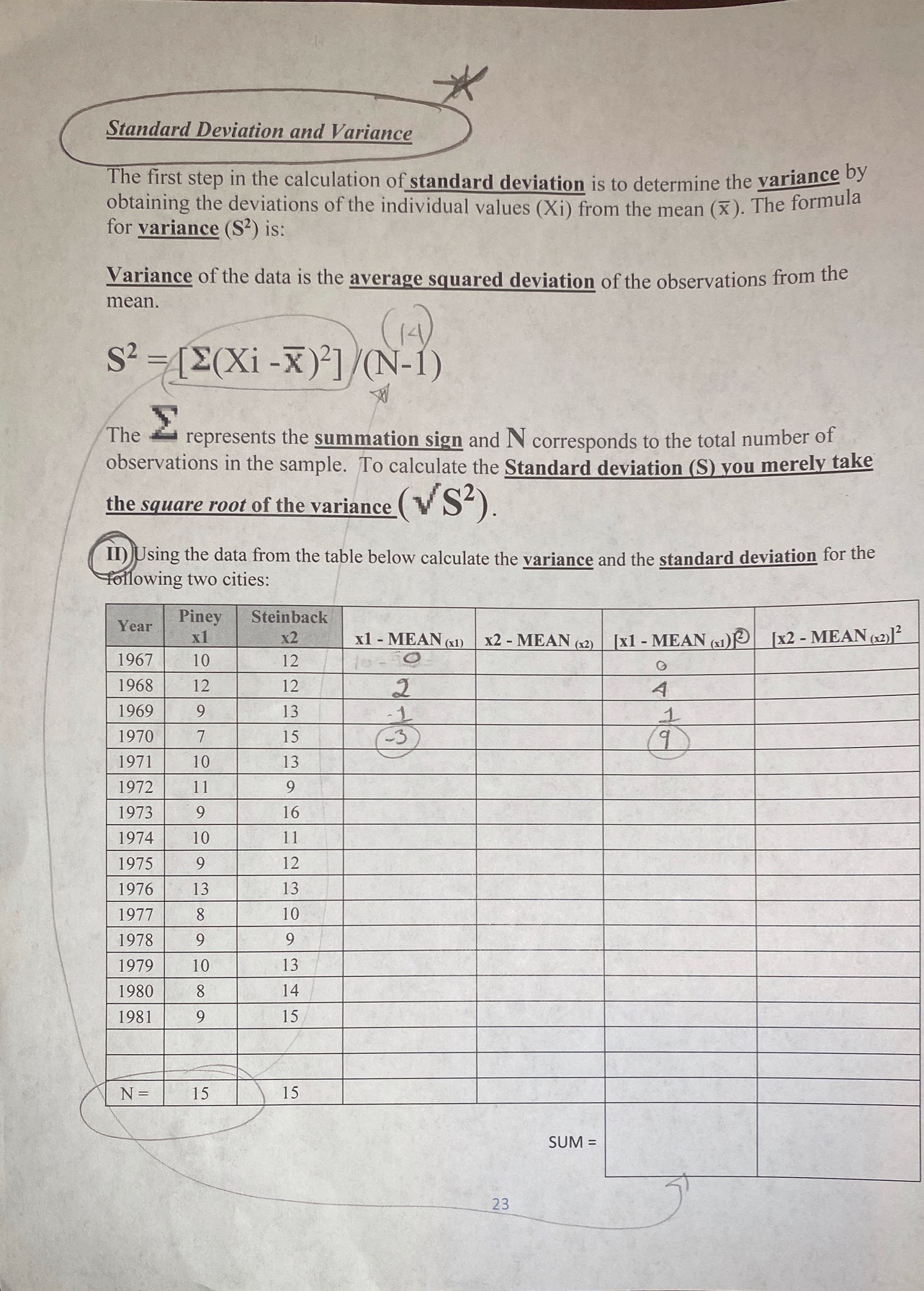
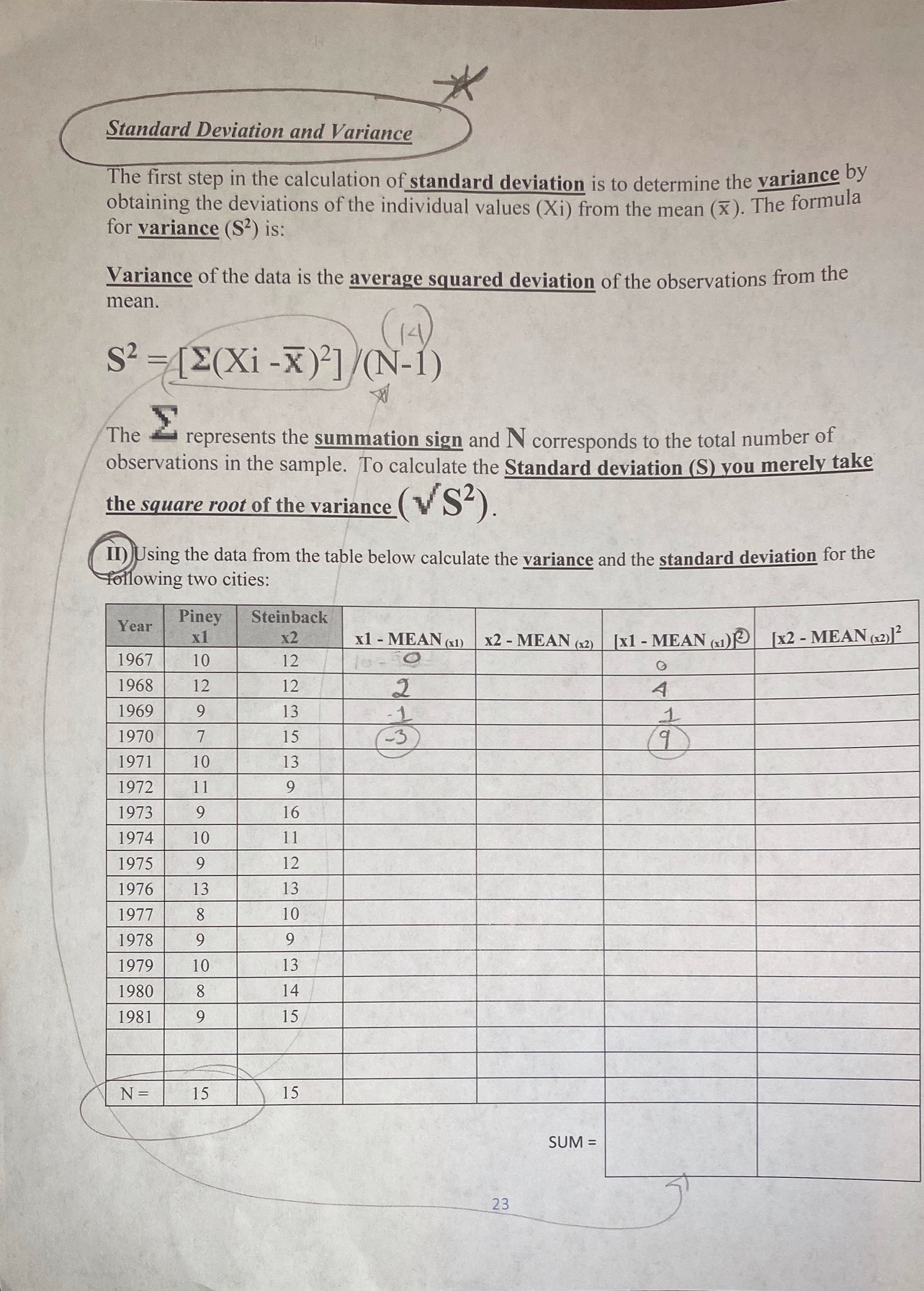
Standard Deviation and Variance The first step in the calculation of standard deviation is to determine the variance by obtaining the deviations of the individual values (Xi) from the mean (x). The formula for variance ($2) is: Variance of the data is the average squared deviation of the observations from the mean. $2 = [E(Xi - x ) ] /( N-1) 14 The represents the summation sign and N corresponds to the total number of observations in the sample. To calculate the Standard deviation (S) you merely take the square root of the variance ( $2). II) Using the data from the table below calculate the variance and the standard deviation for the following two cities: Year Piney Steinback X2 x1 - MEAN (x1) X2 - MEAN (x2) [x1 - MEAN (x1) [x2 - MEAN (x2) 12 1967 10 12 O 1968 12 12 4 1969 9 13 1 1970 7 15 - 3 9 ) 1971 10 13 1972 11 9 1973 9 16 1974 10 11 1975 9 12 1976 13 13 1977 8 10 1978 9 9 1979 10 13 1980 8 14 1981 9 15 N = 15 15 SUM = 23