Standing Waves and Wave Interference

Background

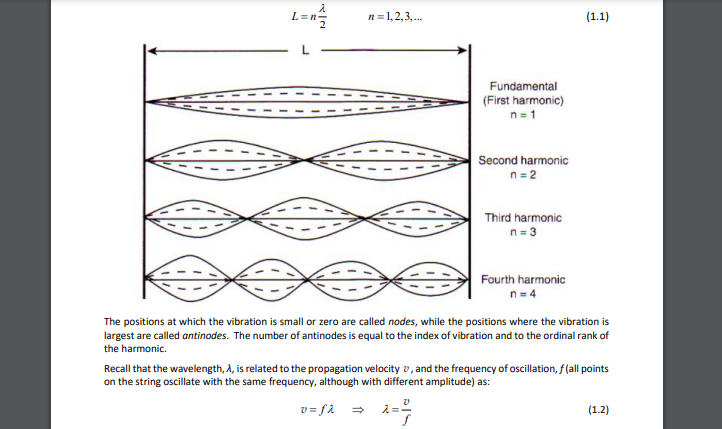
A right-moving incident wave y, reflects of the fixed end and a left-moving becomes wave, y', , with the same frequency and amplitude moving left-ward. Vi(x, t) = Asin(kx - wt) V2(x, t) = Asin(kx + wt) The resultant wave, which is the superposition of each wave, is given by ya(x, t) = yi(x, t) + yz(x,t) = Asin(kx - wt) + Asin(kx + wt) We can rewrite using the trigonometric identity Asin(a) + Asin(B) = 2Asin(- 2 )cos( 7By Va(x, t) = 2Asin(kx)cos (wt) Note that the x and / terms are separated such that the resultant wave is no longer traveling. The resultant wave undergoes simple harmonic motion in the y direction with angular frequency w while the maximum amplitude for a given value of x is bounded by |2Asin(kx)| If we fix the two ends of the string and adjust the frequency so that an integral number of half waves fit into its length, then this standing wave is in resonance. The fixed ends impose a boundary condition on the string; its amplitude at the ends must be zero at all times. Thus, we can say that at x = 0 and x = [ (where & is the length of the string), V3 (x = 0, t) = ya(x = L,t) = 0 2Asin(k * 0)cos (wt) = 2Asin(kL)cos (wt) = 0 Which gives us sin(kL) = 0 This equation is a boundary condition which restricts the string to certain modes of vibration. This equation is satisfied only when kl = ni, where n is the index of vibration (mode) and is equal to any positive integer. In other words, the possible values of & or _ for any given & are KL = () L = nn (n=1,2,3...) or 1 = 21 In the first half of this lab the medium we use is a string fixed at both ends. Setting up standing waves on a string corresponds to creating musical notes on string instruments, such as a guitar or violin". The simplest standing wave formed on a string is half of a wavelength long. This is called the fundamental or 1" harmonic frequency. The next easiest standing wave to create is one that is a full wavelength long. This pattern repeats, and standing waves appear when an integer multiple of half the wavelength exactly fits on the string. InL=n- 1 =1,2,3,... (1.1) L Fundamental (First harmonic) n = 1 - Second harmonic n = 2 Third harmonic n =3 Fourth harmonic n =4 The positions at which the vibration is small or zero are called nodes, while the positions where the vibration is largest are called antinodes. The number of antinodes is equal to the index of vibration and to the ordinal rank of the harmonic. Recall that the wavelength, 1, is related to the propagation velocity , and the frequency of oscillation, f (all points on the string oscillate with the same frequency, although with different amplitude) as: (1.2)Finally, the velocity of a wave on a string is found to depend on both the tension T of the string and the linear density u (mass per unit length) of the string. The exact relationship is given by (1.3) Use equations (1.1), (1.2) and (1.3) to find the frequency of oscillation in terms of tension, length of the string, linear density and harmonic number. Spatial Wave Interference When waves are being created by two sources, the waves add by superposition. The simplest way to see this is to have two sources that emit the exact same wave separated by a distance. Waves radiate in all directions dz from each source. If a point is located such that the difference in the distances to each source Source 2 Source 1 is equal to an integer number multiple of wavelength, there is completely constructive interference. Constructive Interference1. Use equations (1.1), (1.2), and (1.3) to determine the frequency of a standing wave in terms of the tension, length of the string, linear density and harmonic number. 2. Make sketches (like the one on page 3) of the first 4 harmonics in part B. You do not need to deduce the values of n.(1 = 0, 1, 2, 3, ...) For constructive interference, the intensity is higher than either wave alone. If, however, a point is located such that the difference in the distances to each source is equal to (an integer number + %) multiple of the wavelength, there is completely destructive interference. 1, - d21 = (1+ _ )2 (1= 0,1,2,3,..) Source 1 Source 2 For completely destructive interference, the intensity is is almost zero. Destructive Interference Of course, if the waves meet at some distance other than 180" (n radians) out of phase or completely in phase, the intensity will be somewhere between zero and the sum of the intensities of each wave. The image to the right shows a snapshot of the interference pattern between two sources in sync with a single wavelength (frequency). The green lines represent constructive interference and the red are completely destructive interference. Not all constructive and destructive interference lines are shown, but the pattern should be well evident that they are hyperbolae