Stap $1$

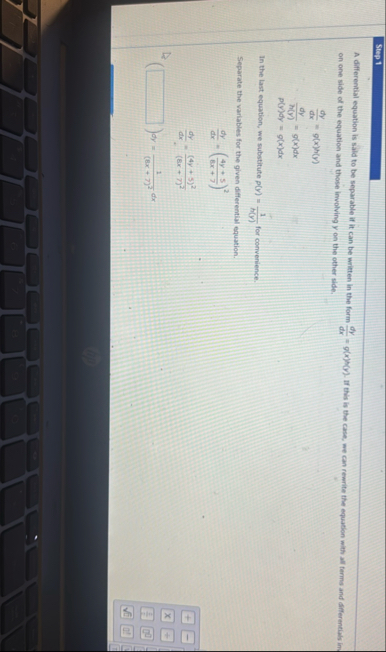
A differential equation is sald to be separable if it can be written in the form $\frac{dy}{dx}=g(x)h(y).$ If this is the case, we can rewrite the equation with all ferms and afferentials in on one side of the equation and those involving $y$ on the other side.

$\frac{dy}{dx}=g(x)h(y)$

$\frac{dy}{h(y)}=g(x)dx$

$p(y)dy=g(x)dx$

In the last equation, we substitute $p(y)=\frac{1}{h(y)}$ for converience.

Separate the variables for the given differential equation.

$\frac{dy}{dx}=(\frac{4y5}{8x7}{)}^2$

$\frac{dy}{dx}=\frac{(4y5{)}^2}{(8x7{)}^2}$

$$

$dy=\frac{1}{(8x7{)}^2}dx$