starter code:

guess_dist = 0 # m guess_angle = 0 # deg guess_m_prop = 0.05 # kg max_dist = 0.0 # change angle iteratively until improvement stops old_guess_dist = guess_dist - 1 while guess_dist >= old_guess_dist: old_guess_dist = guess_dist guess_angle += ??? guess_dist = dist( guess_angle,guess_m_prop ) # ??? # then change m_prop iteratively until improvement stops old_guess_dist = guess_dist - 1 while guess_dist >= old_guess_dist: pass # similar to the above but in guess_m_prop # do not change the angle at all here; just use max_angle # now you should know max_dist, max_angle, max_m_prop

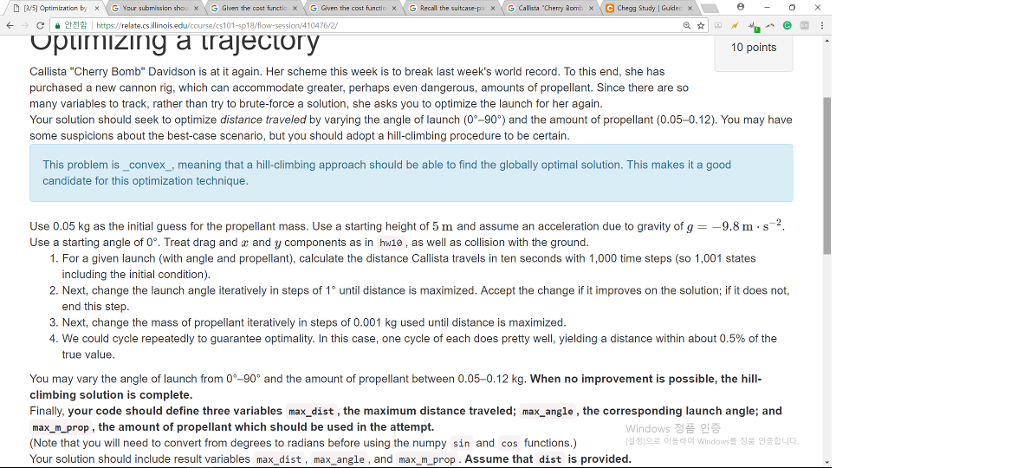
2/5 Optimization by x-G Your submission sho x \ G Gion te cost functic G G r th, cost6netimx \ G Recall th" suitcawp) \ G Calit'dher ygomb X G Chegg Study Guidec ? C ???? ! https://relate.cs.al 101-sp18/fiow-session4 104?6/2/ Opuriizirng a trajectory Callista "Cherry Bomb" Davidson is at it again. Her scheme this week is to break last week's world record. To this end, she has purchased a new cannon rig, which can accommodate greater, perhaps even dangerous, amounts of propellant. Since there are so many variables to track, rather than try to brute-force a solution, she asks you to optimize the launch for her again. Your solution should seek to optimize distance traveled by varying the angle of launch (0-90) and the amount of propellant (0.05-0.12). You may have some suspicions about the best-case scenario, but you should adopt a hill-climbing procedure to be certain. 10 points This problem is_convex, meaning that a hill-climbing approach should be able to find the globally optimal solution. This makes it a good candidate for this optimization technique Use 0.05 kg as the initial guess for the propellant mass. Use a starting height of 5 m and assume an acceleration due to gravity of g =-9.8 m . s-2 Use a starting angle of 0. Treat drag and and y components as in hw1e, as well as collision with the ground. 1. For a given launch (with angle and propellant), calculate the distance Callista travels in ten seconds with 1,000 time steps (so 1,001 states including the initial condition). 2. Next, change the launch angle iteratively in steps of 1 until distance is maximized. Accept the change if it improves on the solution; if it does not, end this step. 3. Next, change the mass of propellant iteratively in steps of 0.001 kg used until distance is maximized 4, we could cycle repeatedly to guarantee optimality. In this case, one cycle of each does pretty well, yielding a distance within about 0.5% of the true value. You may vary the angle of launch from 0-90 and the amount of propellant between 0.05-0.12 kg. When no improvement is possible, the hill climbing solution is complete Finally, your code should define three variables max_dist, the maximum distance traveled; max angle, the corresponding launch angle; and maxm_prop, the amount of propellant which should be used in the attempt. (Note that you will need to convert from degrees to radians before using the numpy sin and cos functions.) Your solution should include result variables max dist, max_ angle, and max _m_prop. Assume that dist is provided Windows ?? ?? [??]?? ???? Windows? ?? ????? 2/5 Optimization by x-G Your submission sho x \ G Gion te cost functic G G r th, cost6netimx \ G Recall th" suitcawp) \ G Calit'dher ygomb X G Chegg Study Guidec ? C ???? ! https://relate.cs.al 101-sp18/fiow-session4 104?6/2/ Opuriizirng a trajectory Callista "Cherry Bomb" Davidson is at it again. Her scheme this week is to break last week's world record. To this end, she has purchased a new cannon rig, which can accommodate greater, perhaps even dangerous, amounts of propellant. Since there are so many variables to track, rather than try to brute-force a solution, she asks you to optimize the launch for her again. Your solution should seek to optimize distance traveled by varying the angle of launch (0-90) and the amount of propellant (0.05-0.12). You may have some suspicions about the best-case scenario, but you should adopt a hill-climbing procedure to be certain. 10 points This problem is_convex, meaning that a hill-climbing approach should be able to find the globally optimal solution. This makes it a good candidate for this optimization technique Use 0.05 kg as the initial guess for the propellant mass. Use a starting height of 5 m and assume an acceleration due to gravity of g =-9.8 m . s-2 Use a starting angle of 0. Treat drag and and y components as in hw1e, as well as collision with the ground. 1. For a given launch (with angle and propellant), calculate the distance Callista travels in ten seconds with 1,000 time steps (so 1,001 states including the initial condition). 2. Next, change the launch angle iteratively in steps of 1 until distance is maximized. Accept the change if it improves on the solution; if it does not, end this step. 3. Next, change the mass of propellant iteratively in steps of 0.001 kg used until distance is maximized 4, we could cycle repeatedly to guarantee optimality. In this case, one cycle of each does pretty well, yielding a distance within about 0.5% of the true value. You may vary the angle of launch from 0-90 and the amount of propellant between 0.05-0.12 kg. When no improvement is possible, the hill climbing solution is complete Finally, your code should define three variables max_dist, the maximum distance traveled; max angle, the corresponding launch angle; and maxm_prop, the amount of propellant which should be used in the attempt. (Note that you will need to convert from degrees to radians before using the numpy sin and cos functions.) Your solution should include result variables max dist, max_ angle, and max _m_prop. Assume that dist is provided Windows ?? ?? [??]?? ???? Windows