State the rules of probabilities

How do you define a probability model?

How do you compute probabilities using the empirical method?

How do you compute probabilities using the classical method?

State the generalized addition rule

State the complement rule

When are events independent?

State the multiplication rule for independent events

State the multiplication rule of counting

Give the definition of permutation

Give the definition of combination

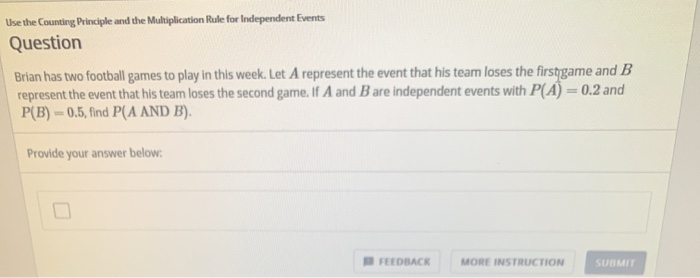
Use the Counting Principle and the Multiplication Rule for Independent Events Question Brian has two football games to play in this week. Let A represent the event that his team loses the firstgame and B represent the event that his team loses the second game. If A and B are independent events with P(A) = 0.2 and P(B) = 0.5, find P( A AND B). Provide your answer below: FEEDBACK MORE INSTRUCTION SUBMITEvent Probability Joint probability : two events occurring together Model A successful 0.7 Model B successful 0.8 P(An B) = P(A) . P(B| A) P(Model B successful | Model A successful) 0.9 P(A and B) = P(A). P(B given A) a. Assume independent * Multiplication Rule for Independent Events P(Model A AND Model B successful) P(An B) = P(A) .P(B) b. Not independent P(Model A AND Model B successful) P(A and B) = P(A) . P(B )7. (2) Suppose that 50% of students carry a Visa credit card, 40% of students carry a MasterCard credit card, and 10% of students carry both Visa and MasterCard. We choose a student at random. Show that the events {selected student carries a Visa} and {selected student carries a MasterCard} are not independent by (a) using the definition of independent events (P(A| B)=P(A)) and by (b) showing that the multiplication rule for independent events does not hold