Steel Rule Deformation Analysis

P: Applied point load $($ N or $kg*\frac{m}{s^2}).$

x : Distance from the fixed end to the point of interest $($ m or cm $).$

L: Total length of the cantilever beam $($ m or cm $).$

E: Young's modulus of the material $($ Pa or $\frac{N}{m^2}).$

I: Moment of inertia of the beam's cross$-$sectional area $(m^4).$

Where:

$P=4\mathrm{.}905N$

$L=0\mathrm{.}30m$

$E=21011\frac{N}{m}2($Young$\text{'}$s Modulus for steel$)$

$I=210-13m4($Moment of inertia$)$

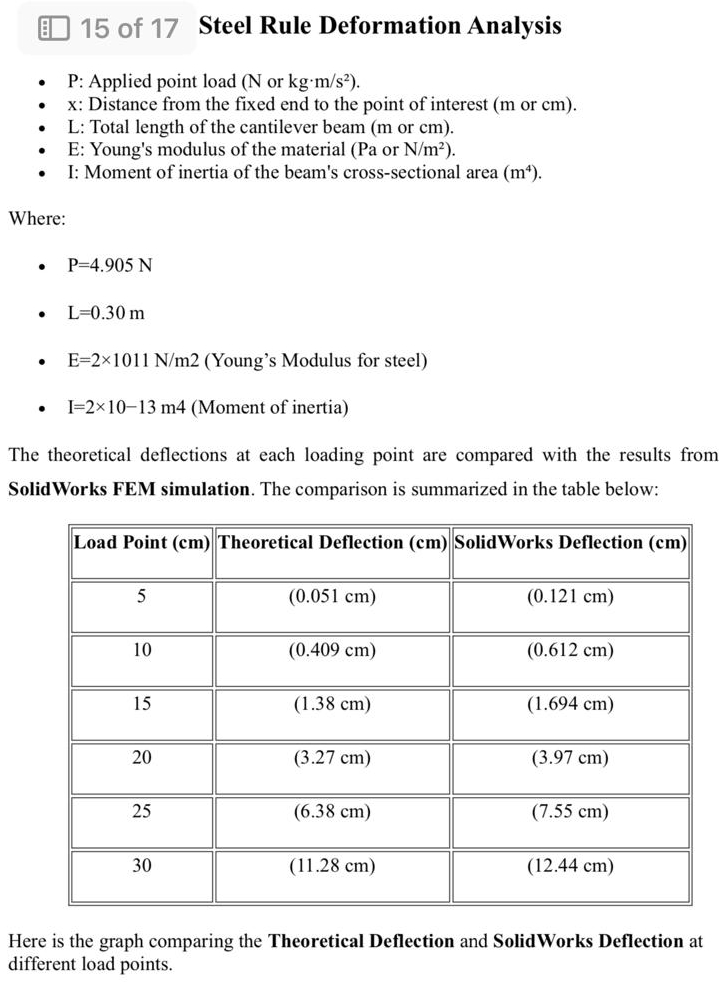
The theoretical deflections at each loading point are compared with the results from

SolidWorks FEM simulation. The comparison is summarized in the table below:

$\backslash$table$[[$Load Point $($cm$),$Theoretical Deflection $($cm$),$SolidWorks Deflection $($cm$)],[5,(0\mathrm{.}051cm),(0\mathrm{.}121cm)$

Calculation Using above tabl:

A$)$ Calculate the deformation at various points along the beam using beam deflection formulas, such as:

delta $=($F $*$ L$^3)/(3*$ E $*$ I$)($for a cantilever beam, point load at end$)$

where:

F $=$ Force applied.

L $=$ Length of the beam.

E $=$ Modulus of elasticity of the beam material.

I $=$ Moment of inertia of the beam cross$-$section.

B$)$ Compute the standard deviation of the measured deflections to understand experimental variability.

NOTE: IF YOU SOLVE CORRECT A&B THEN I WILL GIVE YOU GOOD REVIEW