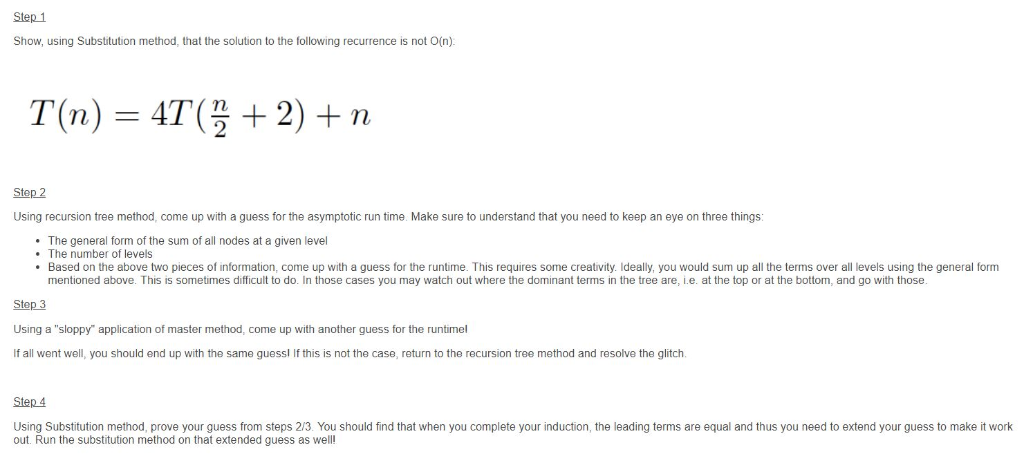
Step 1 Show, using Substitution method, that the solution to the following recurrence is not O(n) Step 2 Using recursion tree method, come up with a guess for the asymptotic run time Make sure to understand that you need to keep an eye on three things . The general form of the sum of all nodes at a given level . The number of levels .Based on the above two pieces of information, come up with a guess for the runtime. This requires some creativity. Ideally, you would sum up all the terms over all levels using the general form mentioned above. This is sometimes difficult to do. In those cases you may watch out where the dominant terms in the tree are, i.e. at the top or at the bottom, and go with those. Step 3 Using a "sloppy" application of master method, come up with another guess for the runtimel If all went well, you should end up with the same guessl If this is not the case, return to the recursion tree method and resolve the glitch Step4 Using Substitution method, prove your guess from steps 2/3. You should find that when you complete your induction, the leading terms are equal and thus you need to extend your guess to make it work out. Run the substitution method on that extended guess as well! Step 1 Show, using Substitution method, that the solution to the following recurrence is not O(n) Step 2 Using recursion tree method, come up with a guess for the asymptotic run time Make sure to understand that you need to keep an eye on three things . The general form of the sum of all nodes at a given level . The number of levels .Based on the above two pieces of information, come up with a guess for the runtime. This requires some creativity. Ideally, you would sum up all the terms over all levels using the general form mentioned above. This is sometimes difficult to do. In those cases you may watch out where the dominant terms in the tree are, i.e. at the top or at the bottom, and go with those. Step 3 Using a "sloppy" application of master method, come up with another guess for the runtimel If all went well, you should end up with the same guessl If this is not the case, return to the recursion tree method and resolve the glitch Step4 Using Substitution method, prove your guess from steps 2/3. You should find that when you complete your induction, the leading terms are equal and thus you need to extend your guess to make it work out. Run the substitution method on that extended guess as well