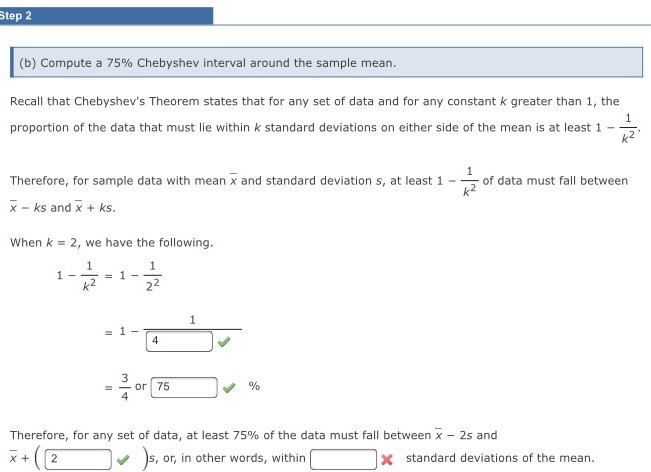
Step 2 (b) Compute a 75% Chebyshev interval around the sample mean. Recall that Chebyshev's Theorem states that for any set of data and for any constant * greater than 1, the proportion of the data that must lie within k standard deviations on either side of the mean is at least 1 Therefore, for sample data with mean x and standard deviation s, at least 1 - * 2 of data must fall between x - ks and x + ks. When k = 2, we have the following. 1 =1 - 1-2 1 =1 - A W or 75 Therefore, for any set of data, at least 75% of the data must fall between x - 2s and x + 2 )s, or, in other words, within x standard deviations of the mean