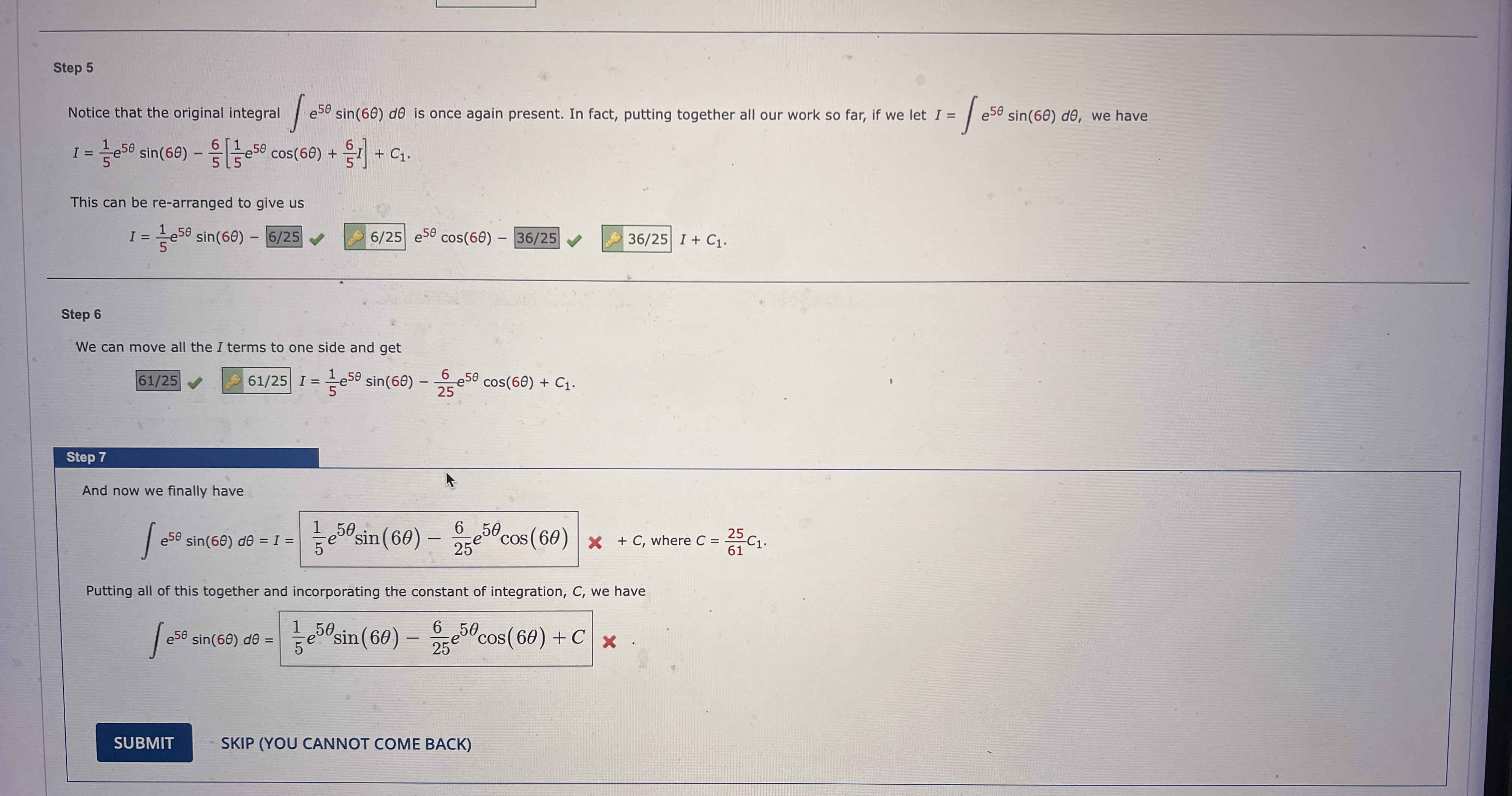
Step $5$

Notice that the original integral ${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}{e}^{5}sin(6)d$ is once again present. In fact, putting together all our work so far, if we let $I={\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}{e}^{5}sin(6)d,$ we have

$I=\frac{1}{5}{e}^{5}sin(6)-\frac{6}{5}[\frac{1}{5}{e}^{5}cos(6)+\frac{6}{5}I]+C_1$

This can be re$-$arranged to give us

$I=\frac{1}{5}{e}^{5}sin(6)-\frac{6}{25},e^{5}cos(6)-\frac{36}{25},I+C_1$

Step $6$

We can move all the I terms to one side and get

$\frac{61}{25},I=\frac{1}{5}{e}^{5}sin(6)-\frac{6}{25}{e}^{5}cos(6)+C_1$

Step $7$

And now we finally have

${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}{e}^{5}sin(6)d=I=\frac{1}{5}{e}^{5}sin(6)-\frac{6}{25}{e}^{5}cos(6),x+c,$ where $c=\frac{25}{61}{c}_1$

Putting all of this together and incorporating the constant of integration, $C,$ we have

${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}{e}^{5}sin(6)d=\frac{1}{5}{e}^{5}sin(6)-\frac{6}{25}{e}^{5}cos(6)+Cx$

$$

SKIP $($YOU CANNOT COME BACK$)$