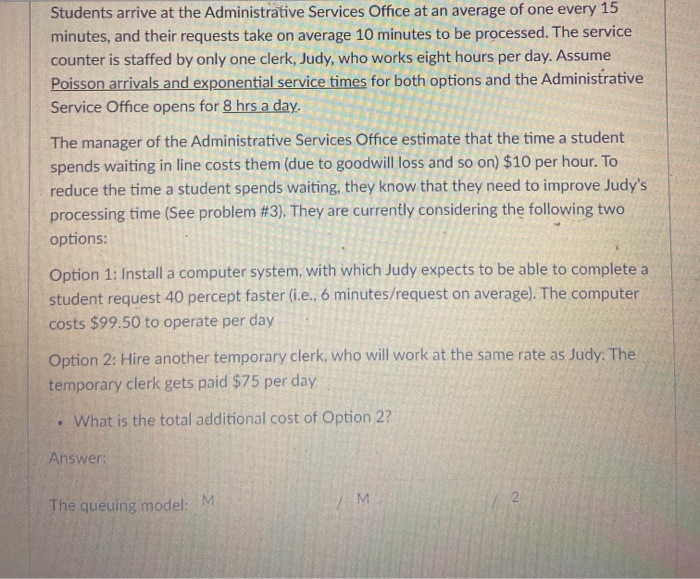
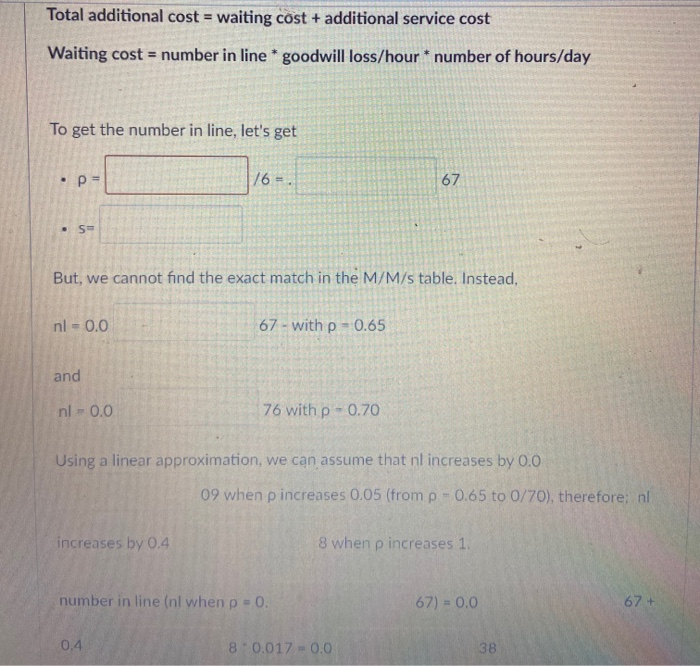
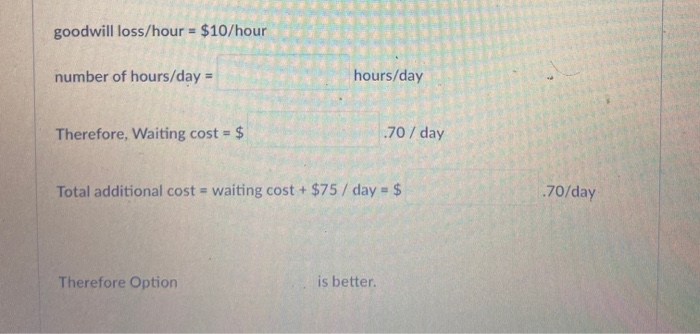
Question: Students arrive at the Administrative Services Office at an average of one every 15 minutes, and their requests take on average 10 minutes to be
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


