study questions for calc

5.)

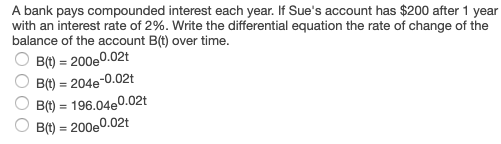
QUESTION 1 If the maximum number of rabbits R, that an area can support is 100, and there are currently 20 rabbits and after 1 month there are 22 rabbits. If the rate of growth of the rabbits is proportional to (100 - R ) and t is measured in months. Write and solve, the differential equation which describes the number of rabbits per month. O R = 80e0.025t O R = 80e0.025t OR = 100-80e-0.025t OR = 100+80e-0.025tQUESTION 2 If rabbits double their population every year. What is the differential equation which describes the rate of change of the rabbit population? Let R(t) be the number of rabbits. O dR dt = R + 2 dR dt = 2R O dR = + 2 O dt dR dtNewton's heating-cooling law, states that the rate of change in the temperature, H, is proportional to the difference between the object and the surrounding temperature. Let H(t) be the temperature of the object being heated and S be the surrounding temperature. If a hot cup of coffee, 170 degrees Fahrenheit, is placed in a 70 degree room. After 20 minutes the cup is 120 degrees. Write and solve the differential equation which describes the temperature of the coffee over time, where time is measured in hours. OH(t) = 70 - 30e-2.079t O H(t) = 70 - 100e-2.079t O H(t) = 70 + 30e-2.079t O H(t) = 70 + 100e-2.079tIf a population of endangered salmon S(t), starts out with 40 fish and decreases proportionally, at a rate of 0.01 fish per year. Write the particular solution to the differential equation which describes the number of fish over time. Let t be measured in years. O S(t) = 40e(-0.04)t O S(t) = 20e(-0.01)t O S(t) = 40e(0.01)t O S(t) = 40e(-0.01)tA bank pays compounded interest each year. If Sue's account has $200 after 1 year with an interest rate of 2%. Write the differential equation the rate of change of the balance of the account B(t) over time. O B(t) = 200e0.02t O Bit) = 204e-0.02t O Bit) = 196.04 0.02t B(t) = 20090.02t