Question: Subject: Stochastic Processes A laboratory blood test is 95% effective in detecting a certain disease when it is actually present. However, the test also yields

Subject: Stochastic Processes

a certain disease when it is actually present. However, the test also

yields a "false positive" result for 1% of the healthy persons tested.

(That is, if a healthy person is tested, then, with probability 0.01,

the test result will imply he has the disease). If 0.5% of

the population actually has the disease, what is the probability a person

has the disease given that his test result is positive? Question 2

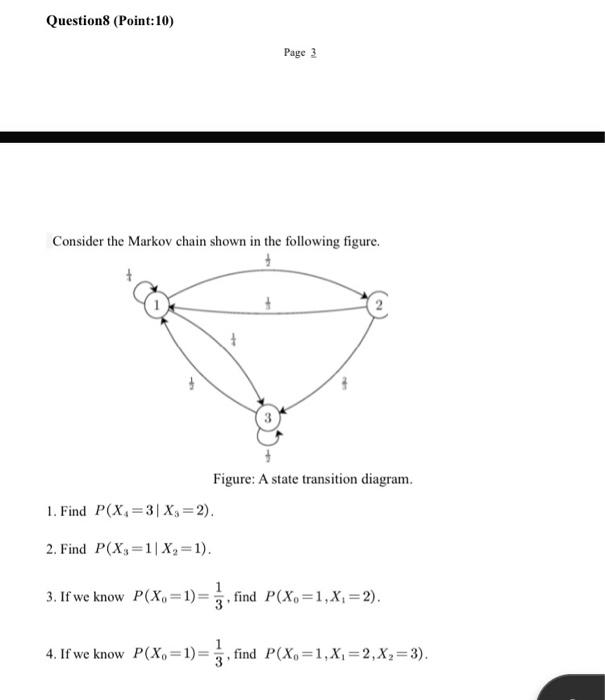
(Point:10) (1) Using the moment generating function calculate the distribution, the mean

and the variance of X+Y, where X and Y are independent and

follow Poisson distributions with two parameters 1 and 2, respectively. (2) Using

A laboratory blood test is 95% effective in detecting a certain disease when it is actually present. However, the test also yields a "false positive" result for 1% of the healthy persons tested. (That is, if a healthy person is tested, then, with probability 0.01, the test result will imply he has the disease). If 0.5% of the population actually has the disease, what is the probability a person has the disease given that his test result is positive? Question 2 (Point:10) (1) Using the moment generating function calculate the distribution, the mean and the variance of X+Y, where X and Y are independent and follow Poisson distributions with two parameters 1 and 2, respectively. (2) Using the moment generating function calculate the distribution, the mean and the variance of X+Y, where X and Y are independent normal random variables with parameters (1,12) and (2,22), respectively. A circuit system is given in the following figure. The reliability (probability of working) of each component is also shown in Figure 1. Assume the components fail independently. (1) What is the probability that the entire system works? (2) Given that the system works, what is the probability that the component A is not working? Figure: Diagram for Question 3. Let X and Y be jointly continuous random variables with joint PDF fX,Y(x,y)={cx+10x,y0,x+y

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

An advantage of MAPE as a measure of forecast error is that: An advantage of MAPE as a measure of forecast error is that: each error is taken as a percent of the previous period forecast so you can...

1. A laboratory blood test is 95% effective in detecting a certain disease when it is, in fact, present. However, the test also yields a false positive result for 1% of the healthy people tested....

A laboratory blood test is 95% effective in detecting a certain disease when it is, in fact, present. In other words, the blood test has 95% sensitivity. However, the test also yields a "false...

Problem 2: A laboratory blood test is 95% effective in detecting a certain disease when it is, in fact, present. However, the test also yields a \"false positive\" result for 1% of the healthy...

hello, i need a expert to do it, thank you> Problem 2: A laboratory blood test is 95% effective in detecting a certain disease when it is, in fact, present. However, the test also yields a \"false...

1.A laboratory blood test is 95% effective in detecting a certain disease when it is, in fact, present. However, the test also yields a false positive result for 1% of the healthy persons tested....

A screening test indicates the presence or absence of a particular disease; such tests are often used by physicians to detect diseases. Suppose that 20% of the population actually has the disease and...

Answer correctly. ICICIUre, A allu b are mutpendent events, Question 5: A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event, 'the number is even,' and B be the event, 'the...

A laboratory blood test is 98% effective in detecting a certain disease if the person has the disease (sensitivity). However, the test also yields a false positive result for 0.5% of the healthy...

A laboratory blood test is 0.95 effective in detecting Corona virus, when it is, in fact, present. However, the test also yields a "false positive" result for 1 percent of the healthy persons tested....

A laboratory blood test is 95 percent effective in detecting a certain disease when it is, in fact, present. however, the last test also yields a "false positive" result for 1 percent of the healthy...

What is the amount and journal entry required? The Note was borrowed on February 1, 2019 and holds interest of 3%. Interest is accrued and not paid at the end of each month (N/12). The first annual...

White light of wavelength ranging from 400 nm to 700 nm is used for a diffraction grating with 6500 lines per centimeter. (a) In a particular order of maximum, red color will have (1) a larger, (2)...

Reduce the cost of capital by increasing the debt to equity ratio.

CT Corp Comprehensive Question Canadian Tire Corporation, Limited (Canadian Tire) is a family of companies that includes a retail segment and a financial services division, among others. The retail...

1. To what extent do you think the organisations mentioned here would benefit from using the Health and Safety Executives stress management standards as a part of their stress policies?

describe the Health and Safety Executives approach to stress management.

3. Do you think that measures of health, safety and wellbeing should be included as a part of the balanced scorecard approach in organisations?