Question: Suppose a company's revenue function is given by R(q) = -q3+ 380q2 and its cost function is given by C(q)=250+18g, where q is hundreds

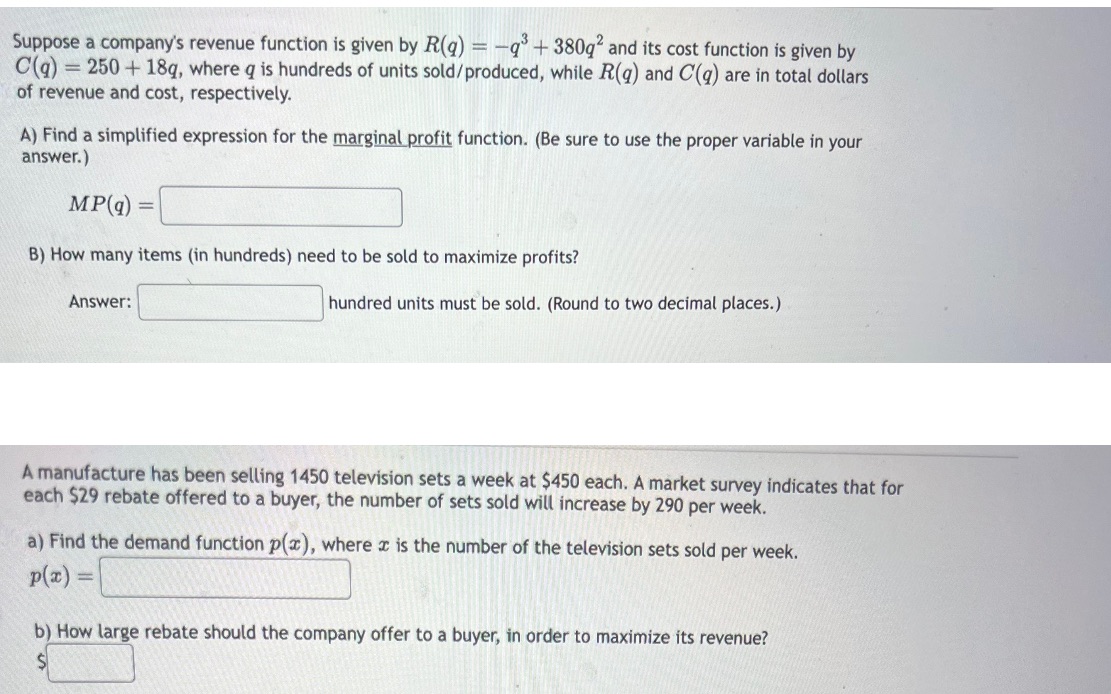
Suppose a company's revenue function is given by R(q) = -q3+ 380q2

Suppose a company's revenue function is given by R(q) = -q3+ 380q2 and its cost function is given by C(q)=250+18g, where q is hundreds of units sold/produced, while R(q) and C(q) are in total dollars of revenue and cost, respectively. A) Find a simplified expression for the marginal profit function. (Be sure to use the proper variable in your answer.) MP(q)= B) How many items (in hundreds) need to be sold to maximize profits? Answer: hundred units must be sold. (Round to two decimal places.) A manufacture has been selling 1450 television sets a week at $450 each. A market survey indicates that for each $29 rebate offered to a buyer, the number of sets sold will increase by 290 per week. a) Find the demand function p(x), where x is the number of the television sets sold per week. p(x) = b) How large rebate should the company offer to a buyer, in order to maximize its revenue?

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Ryan is 26 years old and weighs 213 pounds. He works a full-time construction job during the day and squeezes in online classes at the community college in the evenings. He recently started working...

write results based on this data: BIKE CHOICE X 2=0.35, p=0.55, Cramer's V=0.03 X 2=0.35, padj.=1, Cramer's V=0.03 FOOD CHOICE X 2=0.61, p=.43, Cramer's V=0.04 X 2=0.61, padj.=1, Cramer's V=0.04...

The board of directors declared cash dividends totaling $133,500 during the current year. The comparative balance sheet indicates dividends payable of $30,700 at the beginning of the year and $27,600...

123 Compare the purely graphical properties of these two notations, and the ways in which the graphical properties of each display correspond to the information structure being defined. Describe...

Suppose a company s revenue function is given by R q q 210q and its cost function is given by C q 410 19g where g is hundreds of units sold produced while R q and C q are in total dollars of revenue...

Suppose a company s revenue function is given by R q q 390g and its cost function is given by C q 350 12g where g is hundreds of units sold produced while R q and C q are in total dollars of revenue...

Hi, kindly help me to answer below questions 3 and 5. Thanks! QUESTION 3 a) Find derivatives of the following functions i. Find ifs = (7+9)(#-9). (2.5 marks) ii. Find - if R(x) = 70x' +71x 2x + 2...

Question 1 0/6 pts ) 4 99 0 Details For the given cost function C(a) = 40000 + 600x + x find: a) The cost at the production level 1550 b) The average cost at the production level 1550 c) The marginal...

Question 6 0/2 pts ) 4 99 0 Details A baseball team plays in a stadium that holds 52000 spectators. With the ticket price at $12 the average attendance has been 19000. When the price dropped to $9,...

. Question 9 Glorious Gadgets is a retailer of astronomy equipment. They purchase equipment from a supplier and then sell it to customers in their store. The function O(x) = 4x + 12000x] + 6000...

Is it easy or challenging to enlighten the leadership team, starting with the CEO if a company could implement them?

On May 1, 201X, Leffer Corporation issued $180,000 of 12%, 5-year bonds for $193,918, yielding a market rate of 10%. Interest is paid on October 1 and May 1. Leffer Corporation uses the interest...

Usman and Ahmad, partners in a consulting business, share profits and losses equally. Prior to recording the admission of Ali as a new partner, Usman has a capital balance of $40,000, and Ahmad has a...

* 2256. The electric motor turns an eccentric flywheel which is equivalent to an unbalanced 0.125-kg mass located 250 mm from the axis of rotation. If the static deflection of the beam is 25 mm...

Determine the single equivalent force and the distance from end A to its line of action for the beam and loading shown when (a) 200 B N, F= ↓ MB=100 N m, (b) B 100 N, F= ↑ MB = −600 N...

The three forces and a couple shown are applied to an angle bracket. (a) Find the resultant of this system of forces. (b) Locate the points where the line of action of the resultant intersects line...

A R-12 heat pump cycle shown in Fig P6.47 has a R-12 flow rate of 0.05 kg/s with 4 kW into the compressor. The following data are given Calculate the heat transfer from the compressor, the heat...

In Figure a climber leans out against a vertical ice wall that has negligible friction. Distance a is 0.914 m and distance L is 2.10 m. His center of mass is distance d = 0.940 m from the feet-ground...

Let X, Y, Z be Boolean random variables. Label the eight entries in the joint distribution P (X. Y, Z) as a through h. Express the statement that X and Y are conditionally independent given Z as a...

Design a minimum-mass symmetric three-bar truss (the area of member 1 and that of member 3 are the same) to support a load P, as was shown in Fig. 2.9. The following notation may be used: Pu = P cos...

3 A camera store sells an average of 100 cameras per month. The cost of holding a camera in inventory for a year is 30% of the price the camera shop pays for the camera. It costs $120 each time the...

1 Square City Appliance orders four types of washing machines. Table 7 gives the annual demand, purchasing cost, and annual holding cost (as a percentage of purchase cost), and the fixed cost of...

13 The government is going to build a high-speed computer in Austin, Texas. Once the computer is designed (D), we can select the exact site (S), the building contractor (C), and the operating...