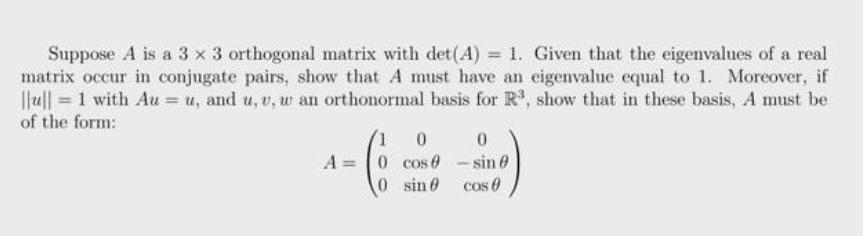
Suppose A is a 3 x 3 orthogonal matrix with det(A) = 1. Given that the eigenvalues of a real matrix occur in conjugate pairs, show that A must have an eigenvalue equal to 1. Moreover, if ||u|| = 1 with Au= u, and u, v, w an orthonormal basis for R, show that in these basis, A must be of the form: 10 0 A=0 cos 0 -sin 0 0 sin cos