Suppose a linear equation is to be fit predicting raw material price as a linear function of the quantity of product A and produce B (made of the same raw material) sold given the following data:

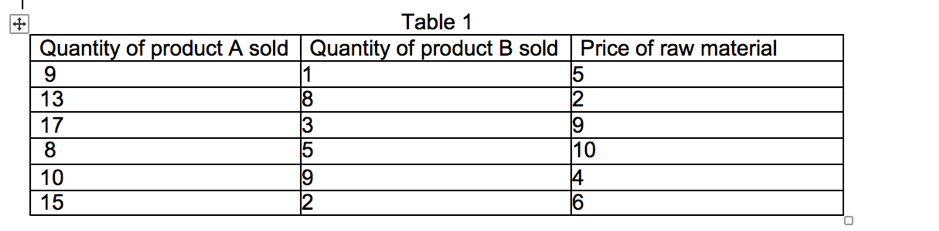
4) Assume we have two additional groups of datasets similar to Table 1, and for each dataset, we have found out their predictions Y = 10 + 18x1 + 17x2, Y2 = 100 + 40x1 + 41x2, Where r", :* (products A and B) are both positive variables and subject to the following constraints: 15x1 + 10x2 S 60 30x1 + 40x2 - 200 - Please develop a LP model to maximise the ratio k = 10+18x1+17%2 100+40x1+41X2 and solvethe formed LP problem using the MATLAB function-linprog. (reference: https://en.wikipedia.org/wiki/Linear-fractional_programming)Table 1 Quantity of product A sold | Quantity of product B sold 9 Price of raw material 13 5 8 2 17 3 9 8 5 10 10 9 15 4 6