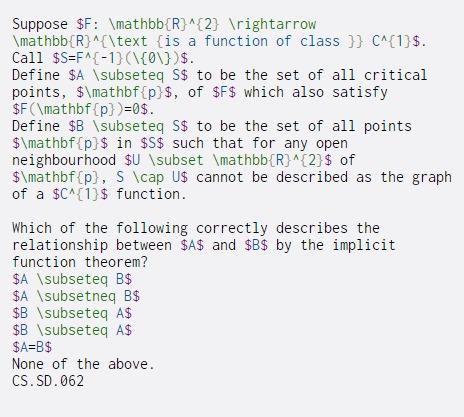
Suppose $F: \mathbb{R}^{2} ightarrow \mathbb{R}^{\text {is a function of class}} C^{1}$. Call $S=F^{-1} ({0\})$. Define $A subseteq S$ to be the set of all critical points, $\mathbf {p}$, of $F$ which also satisfy $FC\mathbf{p})=0$. Define $B \subseteq S$ to be the set of all points $\mathbf{p}$ in $S$ such that for any open neighbourhood $U subset \mathbb{R}^{2}$ of $\mathbf {p}, S \cap U$ cannot be described as the graph of a $C^{1}$ function. Which of the following correctly describes the relationship between $A$ and $B$ by the implicit function theorem? $A \subseteq B$ $A \subsetneq B$ $B \subseteq A$ $B \subseteq A$ $A=B$ None of the above. CS. SD.062