Question: Suppose M is an -NFA with exactly one final state f, but not necessarily satisfying any of our assumptions about the NFA. Make a new

Suppose M is an 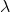Suppose M is an -NFA with exactly one final state -NFA with exactly one final state f, but not necessarily satisfying any of our assumptions about the NFA. Make a new 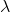-NFA M' by adding two new transitions, 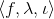and 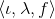, where is the starting state. Is L(M') always equal to L(M)^? ? Either prove that it is or give an example where it is not.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Please do 14.8.4 to prove the following for all strings w. If p is any state of aU Ma (ep, v, D). (Explain why this implies that the language R1 R2 is contained in L(N).) uppose f is a A-NFA with...

answer the question clearly You are building a flight-control system for which a convincing safety case must be made. Would you assign the tasks of safety requirements engineering, test case...

I need the multiple choice questions answers from chapter 4 and 5 of the attached & Monograph...

You are designing a new syntax for a programming language like Java, with the intention of making it more approachable to students by using English words instead of punctuation symbols. (a) How does...

Summarize the following chapter: (Basic Elements of Planning and Decision Making) Obviously, insurance companies incur immense risks because of the number of policies they issue, but you may not know...

Make the summary of the following chapter "Basic Elements of Planning and Decision Making" . Obviously, insurance companies incur immense risks because of the number of policies they issue, but you...

Cash Flows From Working It may surprise you that there are cash flows associated with holding a job. Using the examples provided in Chapter 6, construct a simple cash flow statement and payback...

These two questions is what I will present, and please read through the case first then answer these two questions. Thank you! 1. Suppose you expected the dollar to appreciate in value by 10% against...

Give Correct ANSWERS Human-Computer Interaction (a) If you had been one of the original inventors of the WIMP interface, and engineers on the technical team had been sceptical about the advantages...

Q-1 Read the case properly and elaborate on risk assessment and Link your analysis to Don Rogers feeling about Tetra Techs risk. What has Tetra Tech done to overcome the difficulties associated with...

A large block having the properties of chrome brick at 200C is at a uniform temperature of 30C when it is suddenly exposed to a surface heat flux of 3 104 W/m2. Calculate the temperature at a depth...

Determine the current tax deduction allowed in each of the following situations: a. Sam owns and operates SoftPro, a software programming business. In June, the firm files for bankruptcy. Eighteen...

Casey knows that all imestments come with some level of risk After coploxing different international corporations. This investment comes with its own set of risks. The key risk is that the bonds...

Kirk Van Houten, who has been married for 23 23 years, would like to buy his wife an expensive diamond ring with a platinum setting on their 30 30-year wedding anniversary. Assume that the cost of...