Question: Suppose n > m > 1 are integers such that p = 2m (Znm + 1) 1, q = 2 (2'm + 1) 1, and

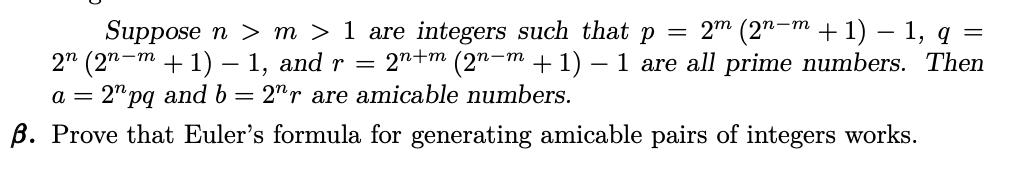
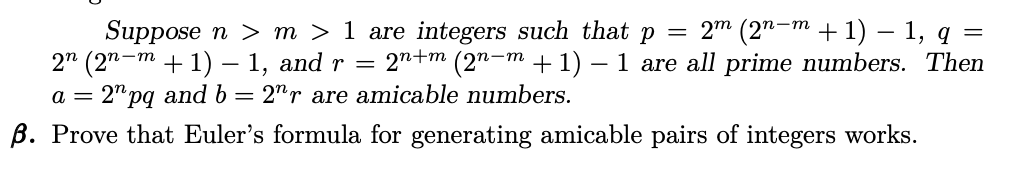
Suppose n > m > 1 are integers such that p

Suppose n > m > 1 are integers such that p = 2m (Znm + 1) 1, q = 2\" (2\"'m + 1) 1, and r : 2n+m (2\"'m + 1) 1 are all prime numbers. Then a : 2\"\"pq and b : 2\"?\" are amicable numbers. ,6. Prove that Euler's formula for generating amicable pairs of integers works

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

A network based service manages persistent objects. The service must enforce an access control policy to protect the objects. (a) Discuss how this access control might best be implemented for the...

HI I need help on what is the answer for this problem. Just the number 5 only. I have answer below but still so unsure. can u help me find the correct answer Problem SPE Q ( x y ) y = ( x + 3 ) P (0...

Give Correct ANSWERS Human-Computer Interaction (a) If you had been one of the original inventors of the WIMP interface, and engineers on the technical team had been sceptical about the advantages...

Hello I am French and I wanted to know if someone could correct questions d), e) and question 2) of this exercise please? We want to show here that there are infinitely many prime numbers that are...

Solve all equestions Consider a Markov chain {Xn, n = 0, 1, . .. } on the state space S = {0, 1, 2}. Suppose that the Markov chain has the transition matrix 0 P = 1 0 0 NIH 1. Show that the state...

This is the code that I currently have. I am unsure on how to do part C or if I even did the first two correctly. Any help would be great! (define (H n) (cond ((= n 0) 1) ((+ (H (- n 1))) (* 2 (P (-...

Learning Objectives Implementing a Menu-Driven Application Modular Programming In class we discussed how functions can be used to do modular programming. Rather than write a program that consists of...

P Moving to another question will save this response Destion 2 points Suppose a stock index contains the stock of 3 firms A, B and C. The stock prices for the three frms are 124, 548 and $51,...

(a) How does the use of condition codes complicate the implementation of a superscalar processor that supports out-of-order execution? [4 marks] (b) A branch predictor with a high prediction accuracy...

EE 351K Probability, Statistics and Stochastic Processes - Spring 2016 Homework 11 Topics: Point estimation, Condence intervals, Random Processes Homework and Exam Grading \"Philosophy\" Answering a...

Your portfolio consists of 250 shares of Stock K with a current market price of $40 per share, 150 shares of Stock Q with a current market price of $25 per share and $8,000 invested in the risk-free...

49.We can say that the allocation of resources is efficient if producer surplus is maximized. b. consumer surplus is maximized. . total surplus is maximized. d. sellers' costs are minimized....

what is the p - value for factor B ( Pressure )

Use Newton's Method to solve the following to a tolerance of 0.001 using the given starting points xg. Provide a table of results and a plot of the iterations. Investigate whether the choice of xo...

PART2 Consider the following LP and its optimal tableau below. Max z = C1X + C2X2 s. t. a11x1 + a12X2 0 X1 X2 S1 S2 1 2 3 5/2 1 3 2 5/2 1 1 1 Determine c1, C2, b1,...

Take Escherichia coli as an example to illustrate the flagellar structure and mechanism of bacterial mobility

Can you please explain what you are doing? 8. A plane perpendicular to the x-y plane contains the point (3, 2, 2) on the paraboloid 36z = 4x? +9y?. The cross-section of the paraboloid created by this...

Can you please explain what you are doing? 9. Suppose the temperature at (x, y, z) is given by T = ry + sin(yz). In what direction should you go from the point (1, 1, 1) to decrease the temperature...

Write a program to wish happy birthday to a student. Firstly, take today month and day as an input and secondly take birthday as an input in the form of month and day. If the input day and month...

Suppose you are an ad-serving company and you have a log of cookie data for ads served to Web pages of all your customers (Amazon, Facebook, etc.). a. Describe, in general terms, how you can process...

Apply ethical tests to management decision-making activities.

Suppose you are an ad-serving company and you maintain a log of cookie data for ads you serve to Web pages for a particular vendor (say Amazon). a. How can you use this data to determine which are...