Question: Suppose that a continuous function f has a derivative f' whose graph is shown below over the interval (1, 10). 5 4 y =f'(x)

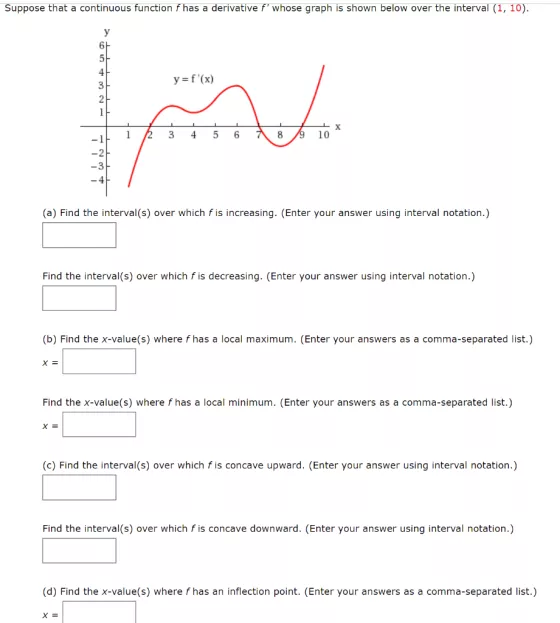
Suppose that a continuous function f has a derivative f whose graph is shown below over the interval (1, 10). y=f(x) 1 2 3

Suppose that a continuous function f has a derivative f' whose graph is shown below over the interval (1, 10). 5 4 y =f'(x) 3 2 4. 6. 8. 9 10 -1 -3 (a) Find the interval(s) over which f is increasing. (Enter your answer using interval notation.) Find the interval(s) over which f is decreasing. (Enter your answer using interval notation.) (b) Find the x-value(s) where f has a local maximum. (Enter your answers as a comma-separated list.) Find the x-value(s) where f has a local minimum. (Enter your answers as a comma-separated list.) (c) Find the interval(s) over which f is concave upward. (Enter your answer using interval notation.) Find the interval(s) over which f is concave downward. (Enter your answer using interval notation.) (d) Find the x-value(s) where / has an inflection point. (Enter your answers as a comma-separated list.)

Step by Step Solution

★★★★★

3.41 Rating (164 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

As diven graph is curue of derivative of PeX so a Using The gir... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mechanical Engineering Questions!

Suppose that a continuous function is periodic with period 1 and is linear between 0 and 025 and linear between - 0.75 and 0. In addition, it has the value 1 at 0 and 2 at 0.25. Sketch the function...

Suppose that a continuous function is periodic with period 2 and is quadratic between -0.25 and 0.25 and linear between - 1.75 and - 0.25. In addition, it has the value 0 at 0 and 0.0625 at 0.25....

Suppose that a continuous income stream has an annual rate of flow at time t given by f (t) =A, where A is a constant. If the interest rate is r (as a decimal, r 0), compounded continuously, show...

Suppose is a continuous function defined on a closed interval [a, b]. (a) What theorem guarantees the existence of an absolute maximum value and an absolute minimum value for f? (b) What steps would...

Sylvan Inc. entered into a non-cancelable lease arrangement with Breton Leasing Corporation for a certain machine. Bretons primary business is leasing; it is not a manufacturer or dealer. Sylvan will...

A fixed point of a function f is a number in its domain such that f(c) = c. (The function doesnt move ; it stays fixed.) (a) Sketch the graph of a continuous function with domain [0, 1] whose range...

Determine the values of the number for which the function f has no critical number: f(x) = (a2 + a 6) cos 2x + (a 2) x + cos 1

Consider the one-dimensional wall shown in the sketch, which is initially at a uniform temperature T j and is suddenly subjected to the convection boundary condition with a fluid at T . For a...

Let f(x) = -x4 -6x3 + 3x -1. Find the open intervals on which f is concave up (down). Then determine the a-coordinates of all inflection points of f. 1. f is concave up on the intervals 2. f is...

The cooling system in a nuclear submarine consists of an assembly of welded pipes through which a coolant is circulated. Specifications require that weld strength must meet or exceed 150 psi. (a)...

Lever Age pays an 8% rate of interest on $10.30 million of outstanding debt with face value $10.3 million. The firm's EBIT was $1.3 million. a. What is its times interest earned? (Round your answer...

ABC Company has current assets of $100,000 and capital assets of $140,000. Current liabilities are $60,000 and long-term liabilities are $90,000. There is $40,000 in preferred stock outstanding and...

Tamarisk Corporation had income from continuing operations of $10,763,000 in 2025. During 2025, it disposed of its restaurant division at an after-tax loss of $201,600. Prior to disposal, the...

Bonita Corporation had income from continuing operations of $10,615,500 in 2025. During 2025, it disposed of its restaurant division at an after-tax loss of $191,900. Prior to disposal, the division...

O'Hara Photography's checkbook lists the following (Click the icon to view the checkbook.) Read the requirements Requirement 1. Prepare O'Hara Photography's bank reconciliation at November 30, 2024....

On January 1, 2022, Blossom Corporation acquired machinery for $1470000. Blossom adopted the straight-line method of depreciation for this machine and had been recording depreciation over an...

Tick the right answer in the multiple-choice questions below. 1. All formulas must begin with: A. = B. + C. D. @ 2. What is the intersection of a column and a row on a worksheet called ? A. Column B....

Describe the Operations (+,,*,/) that can cause negligible addition (NA), error magnification (EM), or subtractive cancellation (SC) in calculating ?((x^2)+1) - x . Give the range of where they might...

Let C be the curve of intersection of a right circular cylinder and a plane making an angle (0

Find the scalar projection of is u = 5i + 5j + 2k on v = - 5i + 5j + k.

In problems, plot a slop field for each differential equation. Use the method of separation fo variables or an integrating factor to find a particular solution of different equation that satisfies...

One of the fust Internet-based groceries home delivery businesses was Homegrocer.com. In 1998, Mike Donald, president of Concord Sales, one of the largest food brokers in B.C., and two partners...

Go to the Web site of Airbus A38G, the biggest passenger plane ever built (525 passengers or more on 2 floors, with a range of 15,000 km, and a wingspan of 80 metres), http://www.airbus....

The fixed cost of running a gift store (wages, rent, etc.) in a particular mall is $250,000 per year. The gross margin (i.e., sales - cost of goods sold or alternatively revenue - variable cost) is...