Suppose that a population grows according $to$ a logistic model with carrying capacity $6500$ and $k=0,0011$ per year.

$(a)$ Write the logistic differential equation for these values.

$\frac{dP}{dt}=0\mathrm{.}0011(1-\frac{P}{6500})P,$ Awesomet

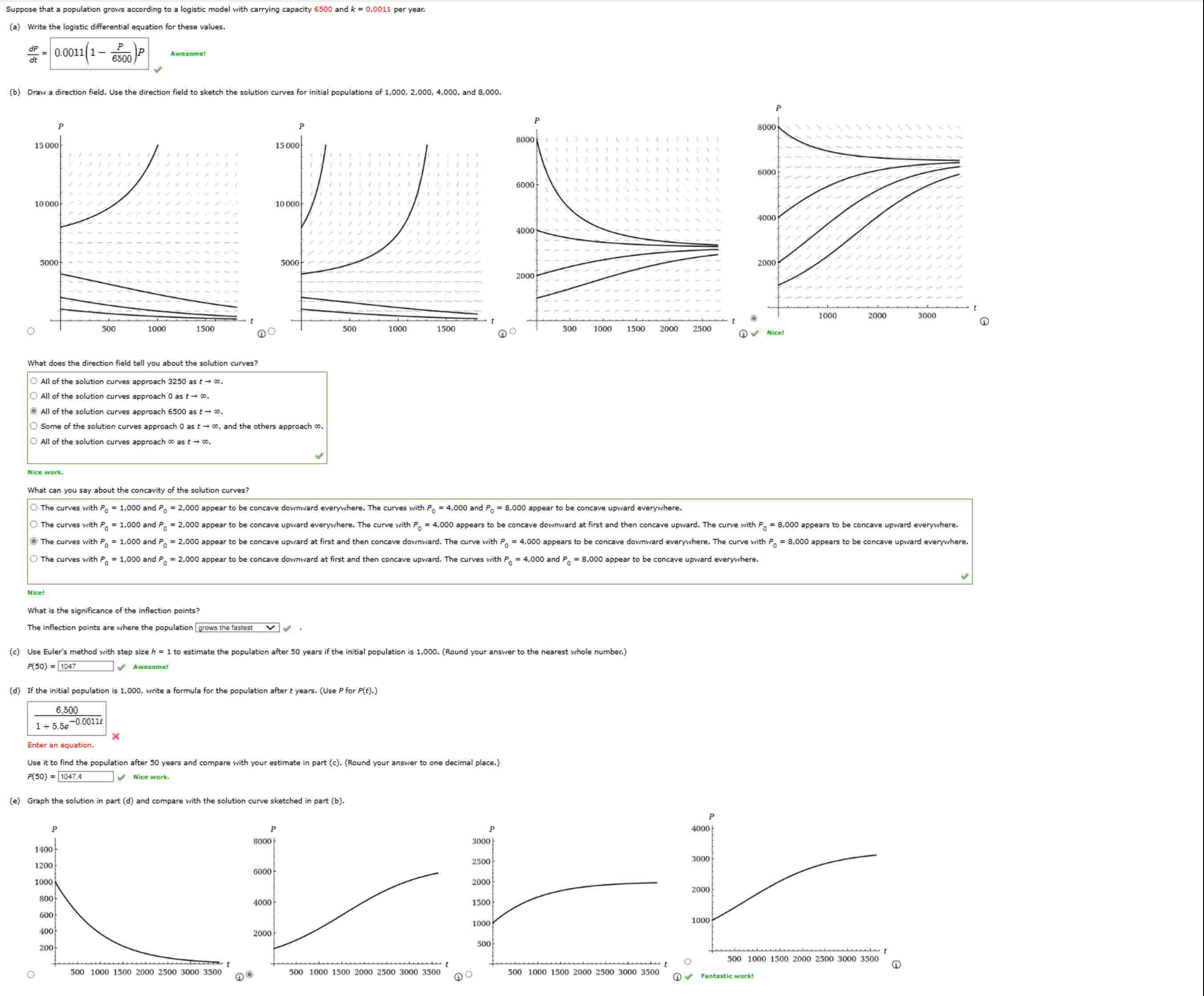
$(b)$ Draw a direction field. Use the direction field $to$ sketch the solution curves for initial populations $of1,000,2,000,4,000,$ and $8,000.$

What does the direction field tell you about the solution curves?

$411of$ the solution curves approach $3250ast.$

All $of$ the solution curves approach $0ast.$

$$ All $of$ the solution curves approach $6500ast.$

Some $of$ the solution curves approach $0ast,$ and the others approach $.$

All $of$ the solution curves approach $ast.$

Nice work.

What can you say about the concavity $of$ the solution curves?

Nicel

What $is$ the significance $of$ the inflection points?

The inflection points are where the population grows the fastest $AA.$

$(c)$ Use Euler's method with step size $h=1to$ estimate the population after $50$ years $if$ the initial population $is1,000.(Round$ your answer $to$ the nearest whole number.$)$

$P(50)=$

$vtP$ for $P(t).\frac{6,500}{1+5\mathrm{.}5e^{-0\mathrm{.}0011t}}$

Enter $an$ equation.

Use $itto$ find the population after $50$ years and compare with your estimate $in$ part $(c).(Round$ your answer $to$ one decimal place.$)$

$P(50)=$

$v$ Nice work.

$(e)$ Graph the solution $in$ part $(d)$ and compare with the solution curve sketched $in$ part $(b).$