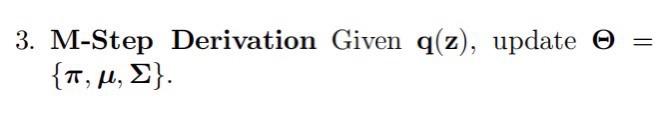
Suppose that a random variable x follows the Gaussian mixture distribution with p(x)= k=1KkN(xk,k). Where ={,,},= {1,,K},={1,,K},={1,,K} and latent variable z Categorical (), where 0,kk=1 1. Likelihood Decomposition. Show that lnp(D;)L(q;),q,, where L(q;)=n=1NEqn(z(n))[ln(qn(z(n))p(x(n),z(n);))] and q(z)=n=1Nqn(z(n)). And, write down the gap between lnp(D;) and L(q;). 2. E-Step Derivation. With given ={,,}, update q(z) 3. M-Step Derivation Given q(z), update = {,,}