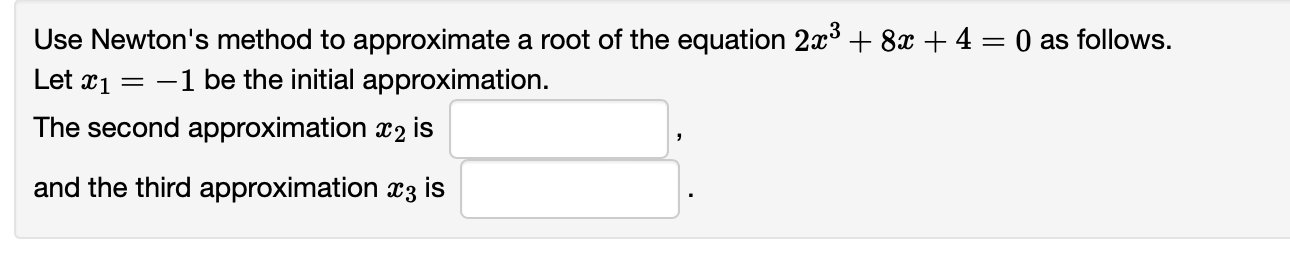
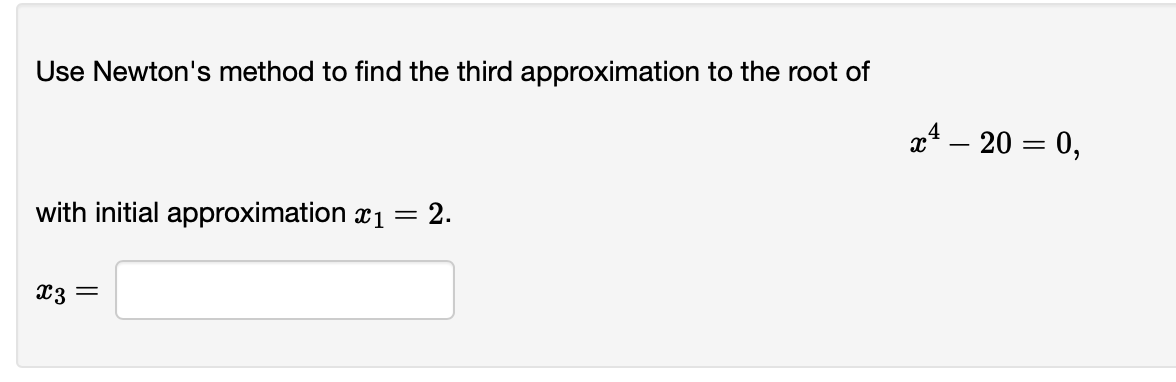
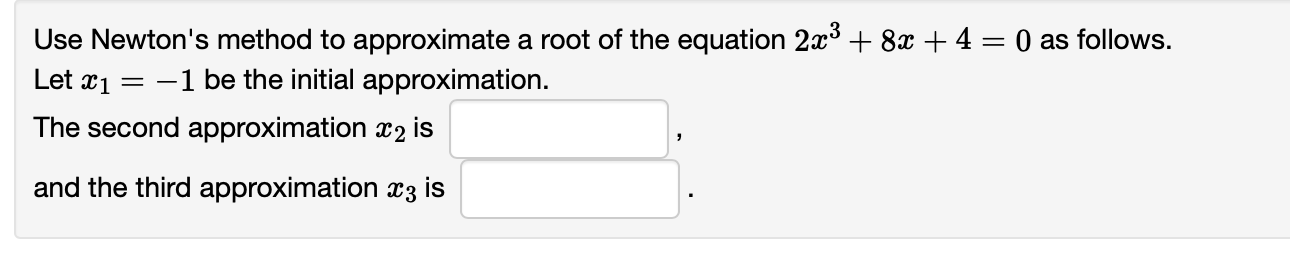
Suppose that an object has position function 3(t) = 3152 2t l 3. Find the average velocity over the interval [3, 6] and find the time at which the instantaneous velocity equals the average velocity. t: See Example 4 page 187 for a similar problem. Consider the function f(:r:) = 2203 62:2 482: + 4 on the interval [5, 8]. Find the average or mean slope of the function on this interval: f(8)-f(-5) _ 8-(-5) _ By the Mean Value Theorem, we know there exists at least one c in the open intewal (55 8) such that f'(c) is equal to this mean slope. Find all values of c that work and list them (separated by commas) in the box below. If there are no values of c that work, enter None. List of numbers: Find the :32 obtained by using Newton's Method to estimate the real root of f (m) = m3 3:1: 5 = 0 when :61 = 4. .712: See Example 2 page 193 for a similar problem. Find the m2 obtained by using Newton's Method to estimate the real root of at) = 2 a: + sin m = 0 with $1 = 3. {132: See Example 3 page 193 for a similar example. Use Newton's method to approximate a root of the equation 23:3 + 8:1: + 4 = 0 as follows. Let ml 2 1 be the initial approximation. The second approximation m2 is , and the third approximation :33 is Use Newton's method to find the third approximation to the root of with initial approximation :31 = 2. 1:3: 20