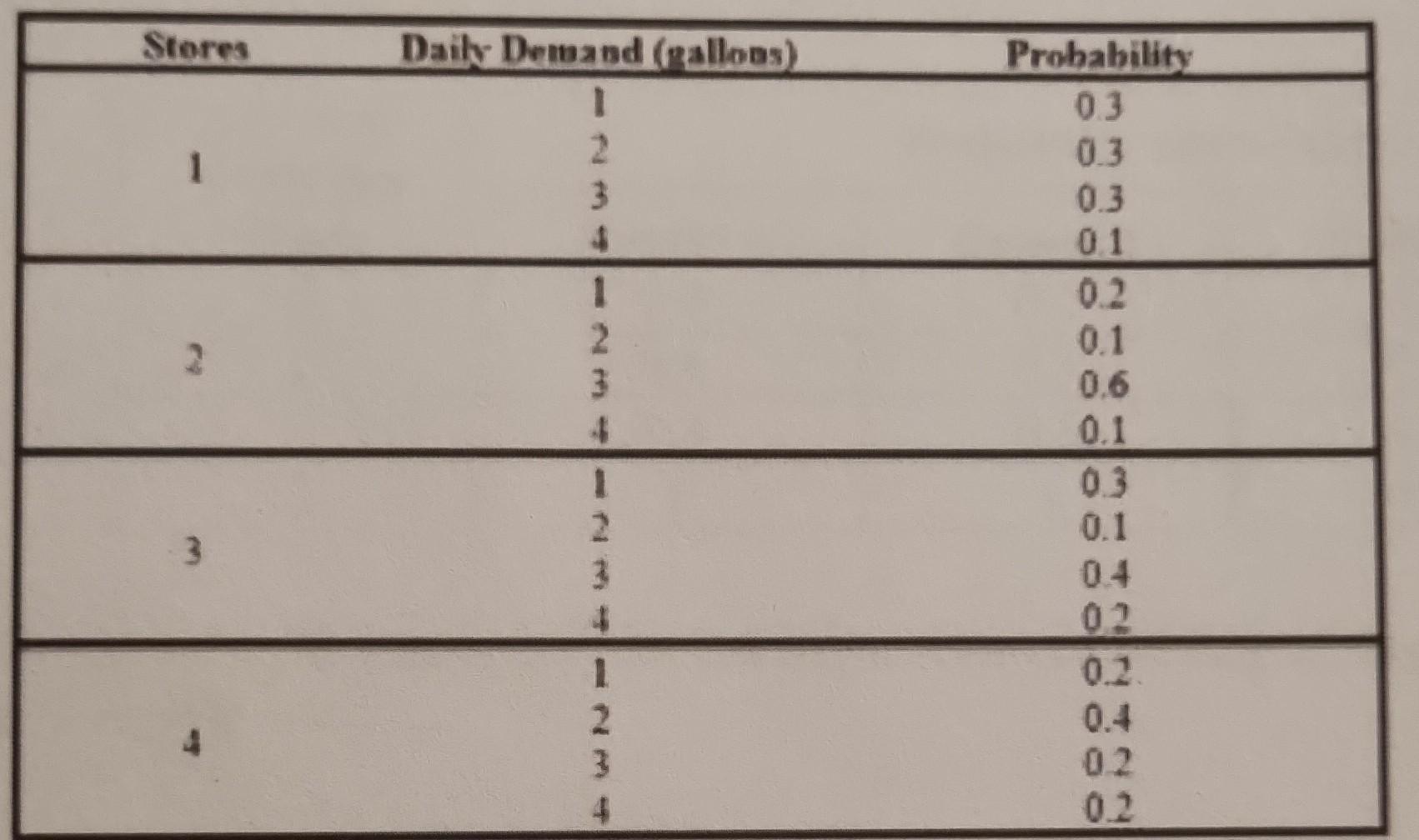
Suppose that by using dynamic programming, we are solving the following milk distribution problem, which as similar to the one that we covered in class. The Celkeg Supermarket chain purchases 5 gallonts of milk from a local dary exeryday. Each gallon of milk is sold in the chain's four stores for 520 gallon. The doiry must bey back for $10 gallon any mulk that is left at the ead of the day. Unfortiaately for Cekce the mill demand for each of the chain's four stotes is uncertain. Past data indicate thas the daily milk demand at each store is as shokn in the following table. Cakco wants to allocate the 5 gallons of mulk to the four stores so as to maximize the expected total daily revenue (aalestsaliatac) earned from milk sales at the four stores. The amount of milk allocated to each store must be an mteger. We use dynamie programming to determine bow Cekce should allocate the 5 galloas of milk among the four steres. Assume that after the distribution of milk to the allocated stores in the morning, no milk will be transferred among the stores. \begin{tabular}{|ccc|} \hline Steres Daify Demand (ralloss) & Probability \\ \hline & 1 & 0.3 \\ 1 & 2 & 0.3 \\ & 3 & 0.3 \\ & 4 & 0.1 \\ \hline 2 & 1 & 0.2 \\ & 2 & 0.1 \\ & 3 & 0.6 \\ & 4 & 0.1 \\ \hline 3 & 1 & 0.3 \\ & 2 & 0.1 \\ & 3 & 0.4 \\ & 4 & 0.2 \\ \hline 4 & 1 & 0.2 \\ & 2 & 0.4 \\ \hline & 4 & 0.2 \\ \hline \end{tabular} Stage t corresponds to store t for every t=1,2,3,4, and the state at a stage is the available amount of milk just before making a decision for the corresponding store. We define the value function f,(i) for the subproblem consisting of stages t,t+1,,4 and the eptimal decision at stage t,xt(i), as ff(i) : the maximum expected total revenue that can be earned by allocating i gallons of milk to stores t. i+1,,4 whers xq(i) : the optumal amount of milk that should be allocated to stote t(tq attain fe(i)) when i gallons of milk is available to allocate to stores t1t+1,,4. Suppose that we have just found that f3(0)=0,f3(1)=20,f3(2)=40,f3(3)=58,f3(4)=75,f3(5)=91. What are the values of f2(3) and x2(3), respectively