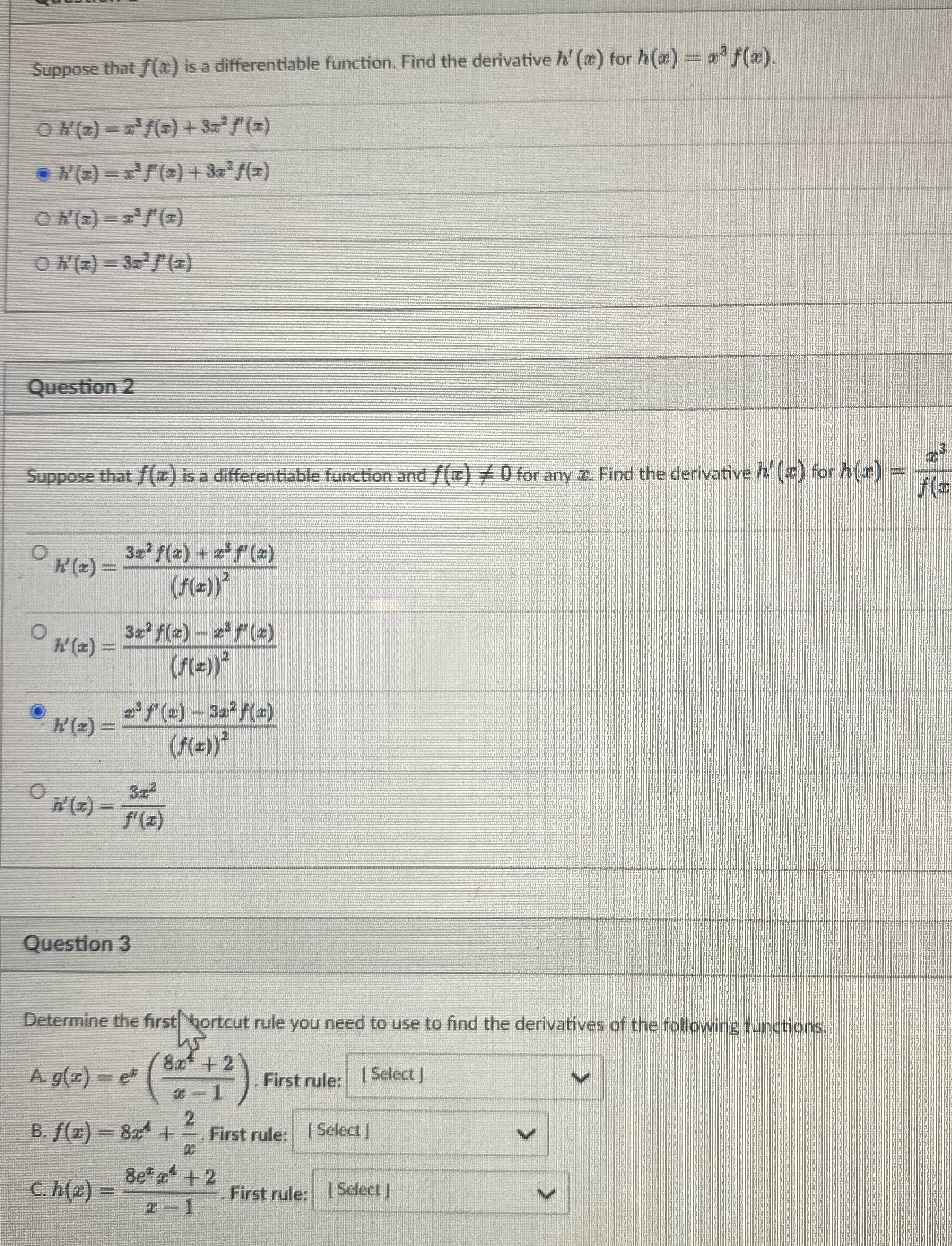
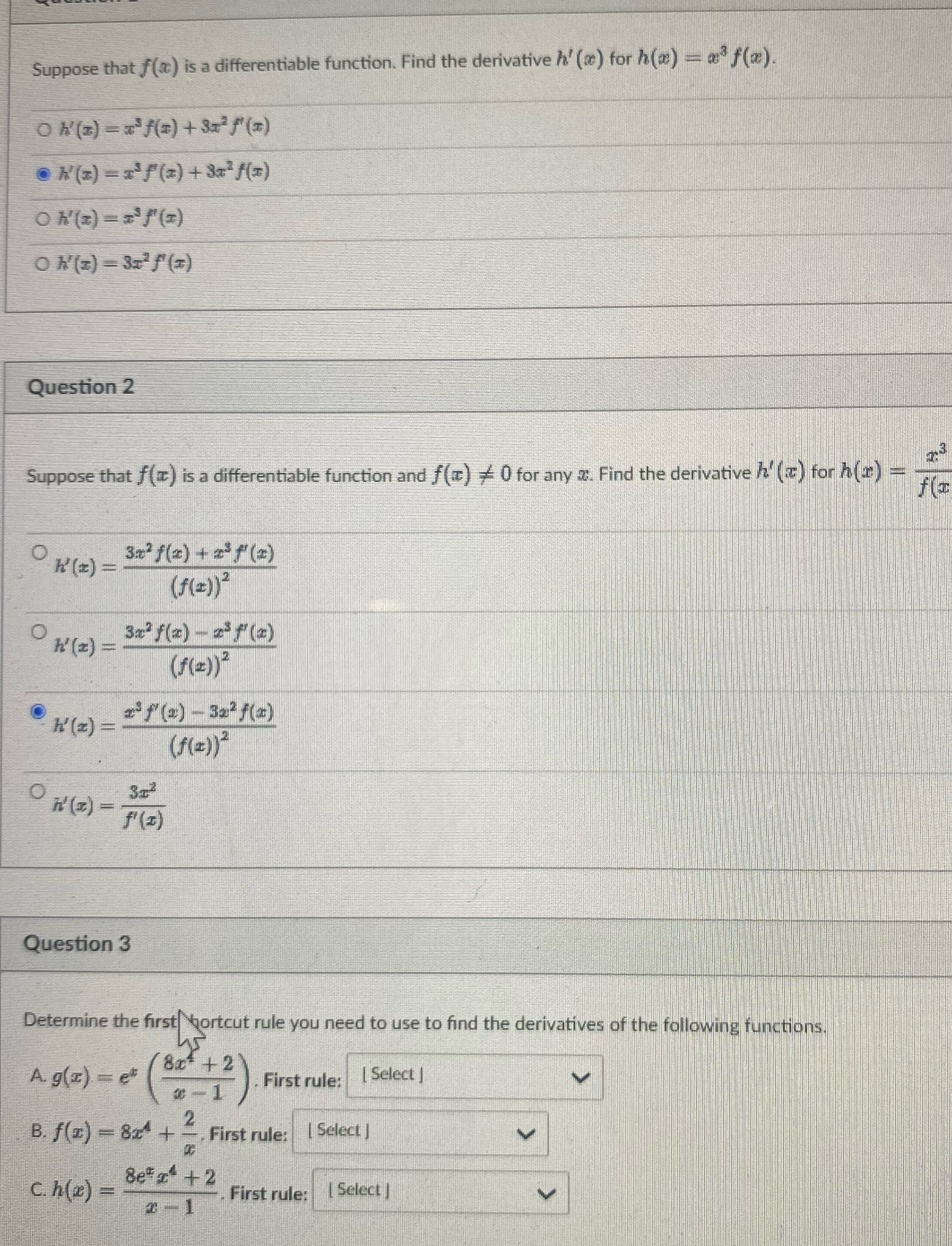
Suppose that f() is a differentiable function. Find the derivative h' (x) for h(2) = a f(z) Oh(z) = x/(2)+ 3x f(7) O N'(z) = x'f(2) + 3x /(2) Oh(z) = 3x f(2) Question 2 Suppose that f(it) is a differentiable function and f () = 0 for any z. Find the derivative It () for h() _ _ O H(z ) = 3x' f (2) + 2 f (2) ( f ( = ) ) OH (z ) = 3x3 f (=) - f() (F(=) OK'(z) = rf (x) -323 /(z) ( f( = ) ) 3x2 O N ( I ) = F (I) Question 3 Determine the first shortcut rule you need to use to find the derivatives of the following functions. A g(z) = 80* + 2 - First rule: [ Select | B. f(x) - 82 + -. First rule: [ Select | C. h() = #+ 2 . First rule: [ Select ) 0-1