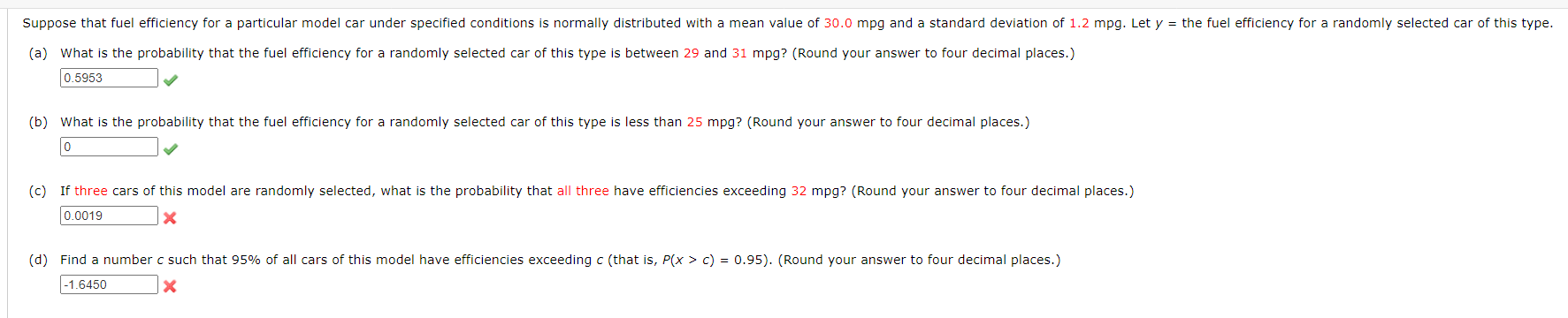
Suppose that fuel efficiency for a particular model car under specified conditions is normally distributed with a mean value of 30.0 mpg and a standard deviation of 1.2 mpg. Let y = the fuel efficiency for a randomly selected car of this type. (a) What is the probability that the fuel efficiency for a randomly selected car of this type is between 29 and 31 mpg? (Round your answer to four decimal places.) 0.5953 (b) What is the probability that the fuel efficiency for a randomly selected car of this type is less than 25 mpg? (Round your answer to four decimal places.) (c) If three cars of this model are randomly selected, what is the probability that all three have efficiencies exceeding 32 mpg? (Round your answer to four decimal places.) 0.0019 X (d) Find a number c such that 95% of all cars of this model have efficiencies exceeding c (that is, P(x > c) = 0.95). (Round your answer to four decimal places.) -1.6450 X