Question: Let A be in Mn (C) with k> n. Prove that there exists no B in Mnk (C) with AB = I. Let A

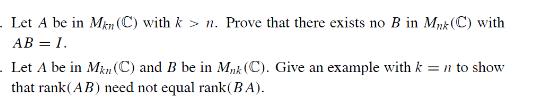
Let A be in Mn (C) with kn. Prove that there exists no B in Mnk (C) with AB = I. Let A be in Min (C) and B be

Let A be in Mn (C) with k> n. Prove that there exists no B in Mnk (C) with AB = I. Let A be in Min (C) and B be in M, (C). Give an example with k = n to show that rank(AB) need not equal rank (BA).

Step by Step Solution

★★★★★

3.42 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To prove that there exists no matrix B in MnC such that AB 1 we can consider the dimensions of the m... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

On January 2, Year 4, Poplar Ltd. purchased 80% of the outstanding shares of Spruce Ltd. for $1,900,000. At that date, Spruce had common shares of $500,000 and retained earnings of $1,150,000 and...

Suppose that in 2010, Global launched an aggressive marketing campaign that boosted sales by 15%. However, their operating margin fell from 5.57% to 4.50%. Suppose that they had no other income,...

Suppose that in 2013, Global launched an aggressive marketing campaign that boosted sales by 15%. However, their operating margin fell from 5.57% to 4.50%. Suppose that they had no other income,...

Suppose that in 2013, Global launches an aggressive marketing campaign that boosts sales by 15%. However, their operating margin falls from 5.57% to 4.50%. Suppose that they have no other income,...

2.9.2 Risk Bounds for the Different Sparsity Settings We consider the linear regression model (2.2). A) Coordinate-sparse setting We focus here on the coordinate-sparse setting. We use the models...

Exercise 16.15. Consider a general stopping problem, where the objective of the individual is to maximize EP t=0 t u (y (t)) . We assume that the individual faces a stream of random variables...

Exercise 21.18. Consider the following non-overlapping generations model, with population normalized 1, where each individual i lives for one period and then begets an offspring. Each individual has...

1.*20. Let (Q,;!f, :?P) be a probability space and .'1+1 a Borel sub field of ;:",h. Prove that there exists a minimal B.F. 9

[19] We investigate the invariance of C under change of program representations from 2-ary to r-ary representations. Let Ar = {0, 1,...,r1}, r 2, and A = N with N the set of natural numbers. A...

[42] Let B be a family of nonempty subsets of {0, 1}n. Let m, k be natural numbers. If a string x of length n is an element of at least 2m sets of complexity at most k in B, then x is an element of a...

5.6.4 Selecting the Number of Steps for the Forward Algorithm We consider the linear regression setting Y = Xb +e = f +e with b 2 Rp and the collection of models fSm : m 2Mg defined in Section 2.2,...

Q. Step 1:H2+IBr-HI+HBr(slow) Step 2:HI+IBr-l2+HBr(fast) A proposed mechanism for the reaction Hz+2IBr-lz+2HBr is shown above. Two experiments were performed at the same temperature but with...

The manufacturer of a product that is subjected to repetitive cycles has specified that the product should be removed from service when any crack reaches 15% of the critical crack length required to...

Emmanuel and Fatima are entering into a bargaining situation in which Emmanuel stands to gain up to $ 5 , 0 0 0 and Fatima stands to gain up to $ 1 , 0 0 0 , provided they reach agreement.Who is...

Write a brief note on the Islams perspectives on risk sharing.

Assignment 1 (COMPULSORY) In the quick-return mechanism represented in figure Q1, the crank OB rotates uniformly at 200 r/min in a clockwise direction about the fixed centre O which is 6,0 cm from...

Discuss how risk should be considered in management decision making; use a real world example to illustrate your discussion.

You work for a corporation as the Vice President for Advertising and Sales as well as serving as an inside director. The corporation is in the business of making and selling custom-designed themed...

Healthcare Financing reference cited needed Discuss the history of Medicare and Medicaid, emphasizing the increasing cost of both programs and what was was the purpose of offering Medicare Advantage...

11.A money multiplier certificate is selling for $8,000 today and promises to be worth $10,000 in 3 years. What is the rate of return on this investment? 11.93% 7.17% 7.72% 19.28%

Suppose that we have a hash table with n slots, with collisions resolved by chaining, and suppose that n keys are inserted into the table. Each key is equally likely to be hashed to each slot. Let M...

Let (x) = x 2 and let RN, LN, and MN be the approximations for the interval [0, 1]. Show that Then, given that the area under the graph of y = x 2 over [0, 1] is 1/3, rank the three approximations...

a. Let A be an m*n matrix, and let B be the result of performing a single elementary row operation on A. Prove that if A not equals to D then B not equals to D. b. LetA be an m*n matrix and let B be...

Quetion 2[20 marks in total ] Consider a model of one-period investment. There are m states on Date 1 and n securities available for trading. Short sales are allowed. Let aij be the unit price of...

[10 marks] Consider the one-period investment problem. There are n securities available on Date 0 and their prices are given by the 1n matrix p. There are m states on Date 1 . The price of Security j...