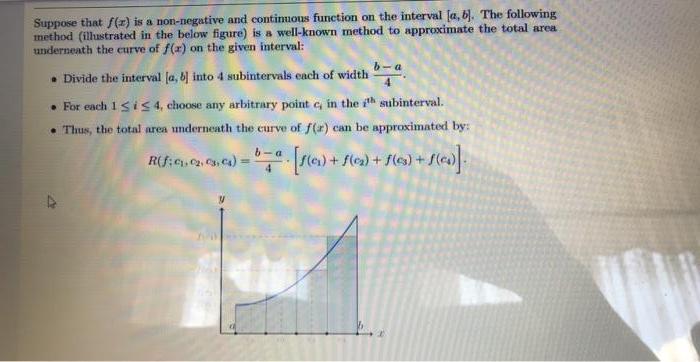
Suppose that f(2) is a non-negative and continuous function on the interval [a, b). The following method (illustrated in the below figure) is a well-known method to approximate the total area underneath the curve of f(x) on the given interval: -a Divide the interval Ja, 6) into 4 subintervals each of width For cach 1sis 4, choose any arbitrary point e, in the h subinterval. Thus, the total area underneath the curve of f(x) can be approximated by: b-a r(e)+fle)+f(es) +.