Question: Suppose that the continuous function f: RR is periodic, that is, there is a number p> 0 such that f(x+p) = f(x) for all

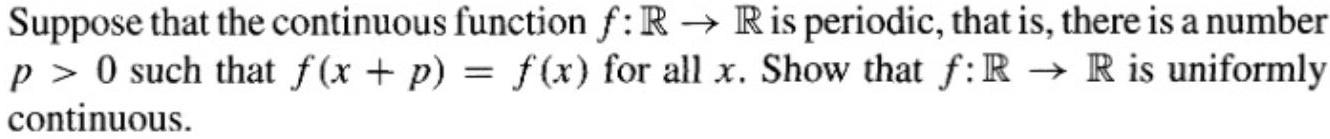
Suppose that the continuous function f: RR is periodic, that is, there

Suppose that the continuous function f: RR is periodic, that is, there is a number p> 0 such that f(x+p) = f(x) for all x. Show that f: RR is uniformly continuous.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Use a definite integral to find an expression that represents the area of the region between the given curve and the x-axis on the interval [0, b]. 15) y=6x Compute the definite integral as the limit...

Please give the solution for this question #3Section 3.5. Guidelines for Sketching a CurveThe following checklist is intended as a guide to sketching a curve y ? f sxd by hand. Not every item is...

1. Suppose that a continuous function f : (a, b) -> R is differentiable except possibly at xo E (a, b), and that lime-+x0 f' (x) = L exists. Prove that f' (To) = L. Warning: It is NOT TRUE in general...

Questions: please solve (ii) In the four-by-four version of the game, starting with pattern explain why it is impossible to reach a pattern with only one white counter. [Hint: don't try to write out...

References: Health Information Management Case Studies Second Edition AHIMA by Dianna M. Foley Health Information Management Technology an Applied Approah Sixth Edition AHIMA by Nanette Sayles and...

D Question 4 2.5 pts Complete the sentence: " For a continuous function f, a point p in the domain of f is an inflection point if..." O f(p) is greater than or equal to the values of f for points...

Digital Signal Processing (a) A radio system outputs signals with frequency components only in the range 2.5 MHz to 3.5 MHz. The analog-to-digital converter that you want to use to digitise such...

Show that every continuous function f : D D on a domain D has a least prefixed point, fix(f). [3 marks] (b) Let h : P P be a continuous function on a domain P. Show that fix(h) = fix(h h). [3 marks]...

Lab-Assignment 2 due 11/30, 2016 Approximation of Functions Recommended Tools: Matlab, Word Staple this page on top of your lab report. Group work done by (list up to 3 names): Lab number Total:...

(a) Fred visits Blotchville again. He finds that the city has installed an electronic display at the bus stop, showing the time when the previous bus arrived. The times between arrivals of buses are...

In a test of controls, auditors may trace receiving reports to vouchers recorded in the voucher register. This is a test for a. Occurrence. b. Completeness. c. Classification. d. Cutoff.

Given the next distance matrix for a TSP with n=5 1) Solve this problem by using B&B, draw the tree and show the excel sheet you will use 2) Solve this problem by using the nearest neighbor 3) Take...

Which life insurance settlement option guarantees payments for the lifetime of the recipient, but also specifies a guaranteed period, during which, if the original recipient dies, the payments will...

Emporia State University sells 4,000 season basketball tickets at $180 each for its 12-game home schedule. Give the entry to record (a) The sale of the season tickets and (b) The revenue earned by...

PepsiCo, Inc.s financial statements are presented in Appendix A. Financial statements of The Coca-Cola Company are presented in Appendix B. Instructions (a) At December 29, 2007, what was PepsiCos...

(a) What are long-term liabilities? Give three examples. (b) What is a bond?

(a) As a source of long-term financing, what are the major advantages of bonds over common stock? (b) What are the major disadvantages in using bonds for long-term financing?

Tim Brown, a friend of yours, has recently purchased a home for $125,000, paying $25,000 down and the remainder financed by a 10.5%, 20-year mortgage, payable at $998.38 per month. At the end of the...

Create a 200 word summary on the Juvenile Justice System than and today. Describe The Juvenile system and provide a generalizable definition. Highlight the issues in the Juvenile system and why this...

Describe the characteristics of an account. LO2

Use horizontal analysis to compare financial statements from different periods. LO7

A debit may signify: LO5 A. an increase in an asset account. B. a decrease in an asset account. C. an increase in a liability account. D. an increase in the owner's capital account.