Suppose that when evaluating an integral, we make the trigonometric substitution

x=sec\\\\theta

.\ Find the value of

ln|sec\\\\theta +tan\\\\theta |-csc\\\\theta +C

in terms of

x

.\

ln|x+(1)/(\\\\sqrt(x^(2)-1))|-(\\\\sqrt(x^(2)-1))/(x)+C\ ln|x+\\\\sqrt(x^(2)-1)|-(x)/(\\\\sqrt(x^(2)-1))+C\ ln|x+(x^(2))/(\\\\sqrt(x^(2)-1))|-(\\\\sqrt(x^(2)-1))/(x^(2))+C\ ln|x+\\\\sqrt(x^(2)-1)|-(\\\\sqrt(x^(2)-1))/(x)+C\ ln|x+(x)/(\\\\sqrt(x^(2)-1))|-(\\\\sqrt(x^(2)-1))/(x)+C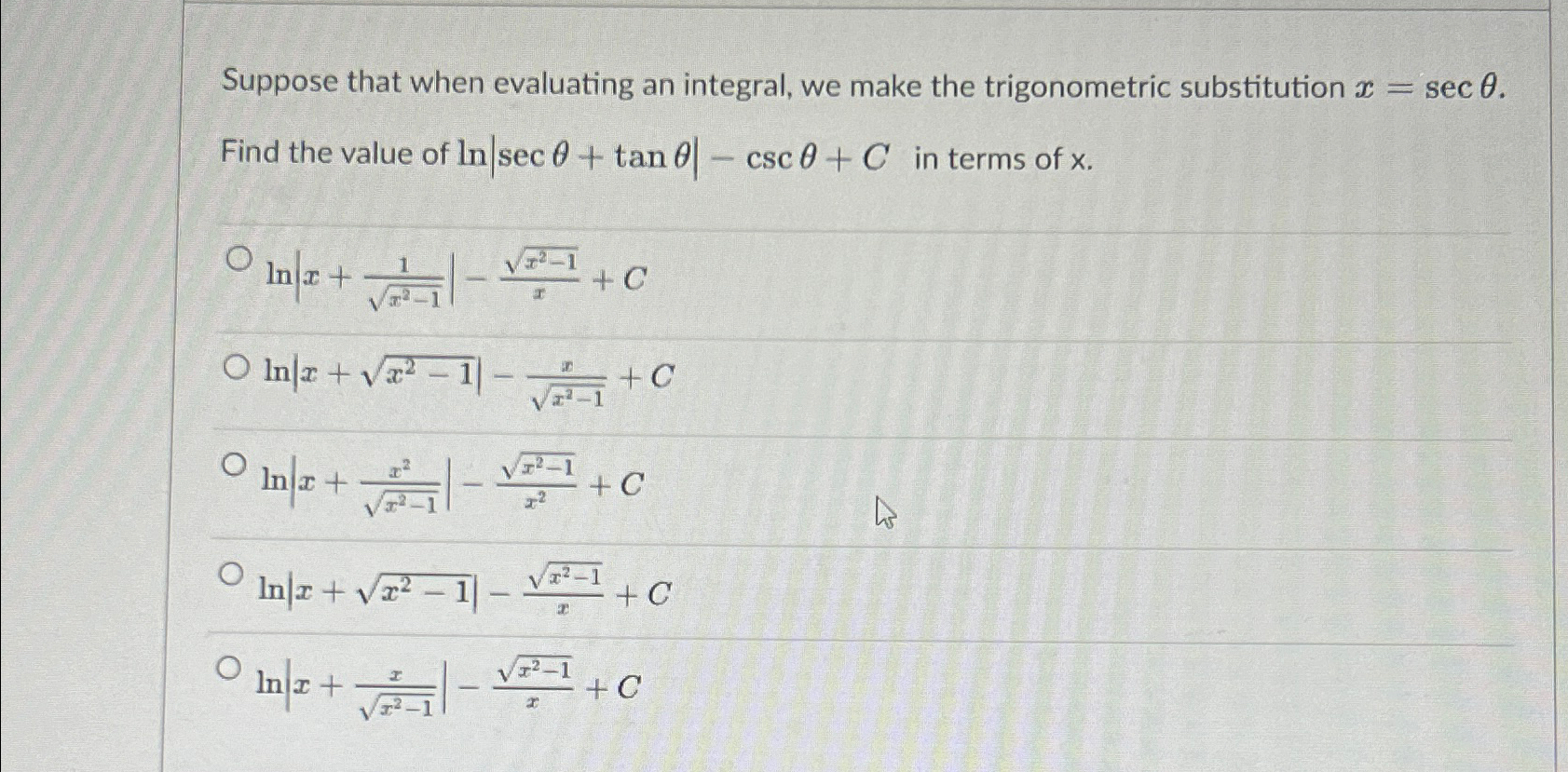

Suppose that when evaluating an integral, we make the trigonometric substitution x=sec. Find the value of lnsec+tancsc+C in terms of x. lnx+x211xx21+Clnx+x21x21x+Clnx+x21x2x2x21+Clnx+x21xx21+Clnx+x21xxx21+C