Question: $$ Suppose that $X$ and $y$ are two random variables whose joint distribution has density f_{XY)(x, y)=left{begin{array}{11} frac{2}{pileft(1+y^{2} ight)} & text { if } 0
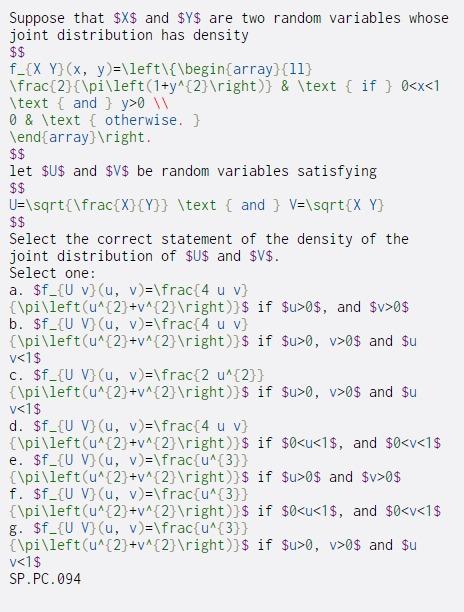
$$ Suppose that $X$ and $y$ are two random variables whose joint distribution has density f_{XY)(x, y)=\left\{\begin{array}{11} \frac{2}{\pi\left(1+y^{2} ight)} & \text { if } 0
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


