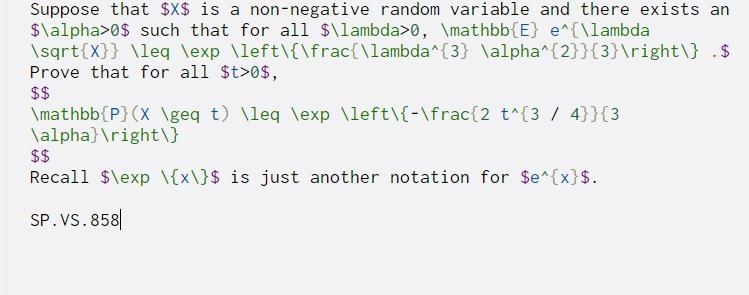
Suppose that $X$ is a non-negative random variable and there exists an $\alpha>0$ such that for all $\lambda>0, \mathbb{E} e^{\lambda \sqrt{X}} \leq \exp \left\{\frac{\lambda^{3} \alpha^{2}}{3} ight\} .$ Prove that for all $t>o$, $$ \mathbb{P}(X \geq t) \leq \exp \left\{-\frac{2 t^{3 / 4}}{3 \alpha} ight) $$ Recall $\exp \{x\}$ is just another notation for $e^{x}$. SP.VS.858