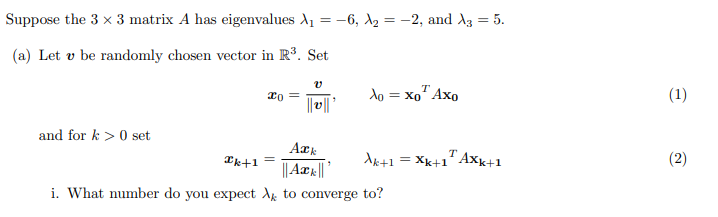
Suppose the 33 matrix A has eigenvalues 1=6,2=2, and 3=5. (a) Let v be randomly chosen vector in R3. Set x0=vv,0=x0TAx0 and for k>0 set xk+1=AxkAxk,k+1=xk+1TAxk+1 i. What number do you expect k to converge to? ii. What number do you expect Axkkxk to converge to? iii. For large k,xk is approximately an eigenvector corresponding to which eigenvalue of A ? (b) Let v be randomly chosen vector in R3. Set x0=vv,0=x0TA1x0 and for k>0 set xk+1=A1xkA1xk,k+1=xk+1TA1xk+1 i. What are the eigenvalues of A1 ? ii. What number do you expect k to converge to? iii. What number do you expect k1 to converge to? iv. For large k,xk is approximately an eigenvector corresponding to which eigenvalue of A ? (c) Let v be randomly chosen vector in R3. Set x0=vv,0=x0T(A+4I)1x0 and for k>0 set xk+1=(A+4I)1xk(A+4I)1xk,k+1=xk+1T(A+4I)1xk+1 i. What are the eigenvalues of A+4I ? ii. What are the eigenvalues of (A+4I)1 ? iii. What number do you expect k to converge to? iv. What number do you expect k14 to converge to? v. For large k,xk is approximately an eigenvector corresponding to which eigenvalue of A