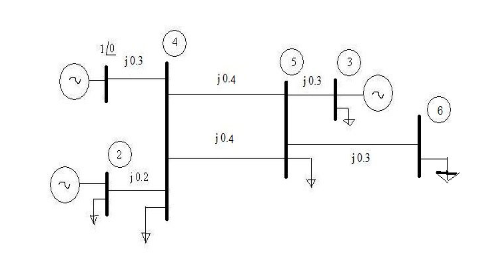
Suppose the following are specified:

PG$2=0\mathrm{.}5,$ V$2=1\mathrm{.}05,$ PG$3=1\mathrm{.}0,$ V$3=1\mathrm{.}06$

PL$2=0\mathrm{.}2,$ PL$3=0\mathrm{.}1,$ PL$4=0\mathrm{.}5,$ PL$5=0\mathrm{.}3,$ PL$6=0\mathrm{.}2$

QL$2=0\mathrm{.}1,$ QL$3=0\mathrm{.}0,$ QL$4=0\mathrm{.}1,$ QL$5=0\mathrm{.}1,$ QL$6=-0\mathrm{.}1$

a$)$ Classify the bus types and write out the power$-$flow equations.

b$)$ Compute the DC power$-$flow solution.

c$)$ Starting from the DC power$-$flow solution, implement the Newton$-$Algorithm till all the power mismatch errors are smaller than $0\mathrm{.}001$ pu$.$ How many iterations does it take to reach convergence?

d$)$ Starting from the DC power$-$flow solution, implement the fast decoupled power$-$flow algorithm until all the power mismatches are smaller than $0\mathrm{.}001$ pu$.$ How many iterations does it take to reach the convergence?

e$)$ Repeat parts b$,$ c and d$,$ when each of the loads PLi and QLi and generations PGi specified become twice the previous values. Comment on your result.

My current code: function $[$ybus$,$ P$\_$eq$,$ Q$\_$eq$,$ theta$]=$ power$\_$flow$\_$analysis$()$

$\%$ Form Ybus matrix and return power flow equations, including DC power flow solution

$\%$ Line data: $[$from$\_$bus, to$\_$bus, R$,$ X$,$ B$/2]$

linedata $=[140\mathrm{.}000\mathrm{.}300\mathrm{.}00$;

$240\mathrm{.}000\mathrm{.}200\mathrm{.}00$;

$450\mathrm{.}000\mathrm{.}400\mathrm{.}00$;

$450\mathrm{.}000\mathrm{.}400\mathrm{.}00$;

$530\mathrm{.}000\mathrm{.}300\mathrm{.}00$;

$560\mathrm{.}000\mathrm{.}300\mathrm{.}00]$;

fb $=$ linedata$($:$,1)$; $\%$ From bus

tb $=$ linedata$($:$,2)$; $\%$ To bus

r $=$ linedata$($:$,3)$; $\%$ Resistance

x $=$ linedata$($:$,4)$; $\%$ Reactance

b $=$ linedata$($:$,5)$; $\%$ Line charging

z $=$ r $+1$i $*$ x; $\%$ Impedance

y $=1./$ z; $\%$ Admittance

b $=1$i $*$ b; $\%$ Ground admittance

nbus $=$ max$($max$($fb$),$ max$($tb$))$; $\%$ Number of buses

nbranch $=$ length$($fb$)$; $\%$ Number of branches

ybus $=$ zeros$($nbus$,$ nbus$)$; $\%$ Initialize Ybus matrix

$\%$ Off$-$diagonal elements

for k $=1$:nbranch

ybus$($fb$($k$),$ tb$($k$))=$ ybus$($fb$($k$),$ tb$($k$))-$ y$($k$)$;

ybus$($tb$($k$),$ fb$($k$))=$ ybus$($fb$($k$),$ tb$($k$))$; $\%$ Symmetric entry

end

$\%$ Diagonal elements

for m $=1$:nbus

for n $=1$:nbranch

if fb$($n$)==$ m $||$ tb$($n$)==$ m

ybus$($m$,$ m$)=$ ybus$($m$,$ m$)+$ y$($n$)+$ b$($n$)$;

end

end

end

$\%$ Display the Ybus matrix

disp$(\text{'}$Ybus Matrix:$\text{'})$;

disp$($ybus$)$;

$\%$ Form the power flow equations for real $($P$)$ and reactive $($Q$)$ power

$[$P$\_$eq$,$ Q$\_$eq$]=$ form$\_$power$\_$flow$\_$equations$($ybus$)$;

disp$(\text{'}$Real Power Equations $($P$)$:$\text{'})$;

disp$($P$\_$eq$)$;

disp$(\text{'}$Reactive Power Equations $($Q$)$:$\text{'})$;

disp$($Q$\_$eq$)$;

$\%$ DC Power Flow Solution with specified power and voltage values

theta $=$ dc$\_$power$\_$flow$($ybus$)$;

disp$(\text{'}$DC Power Flow Voltage Angles $($theta in radians$)$:$\text{'})$;

disp$($theta$)$;

end

function $[$P$\_$eq$,$ Q$\_$eq$]=$ form$\_$power$\_$flow$\_$equations$($ybus$)$

$\%$ Retrieve power flow equations $($real and reactive$)$

n $=$ size$($ybus$,1)$; $\%$ Number of buses

V $=$ sym$(\text{'}$V$\text{'},[$n$,1],$ 'real'$)$; $\%$ Voltage magnitudes

theta $=$ sym$(\text{'}$theta$\text{'},[$n$,1],$ 'real'$)$; $\%$ Voltage angles

$\%$ Initialize symbolic power equations

P$\_$eq $=$ sym$($zeros$($n$,1))$;

Q$\_$eq $=$ sym$($zeros$($n$,1))$;

for i $=1$:n

for j $=1$:n

if i ~$=$ j

$\%$ Contributions to P$\_$i and Q$\_$i from bus j

P$\_$eq$($i$)=$ P$\_$eq$($i$)+$ V$($i$)*$ V$($j$)*...$

$($real$($ybus$($i$,$ j$))*$ cos$($theta$($i$)-$ theta$($j$))+...$

imag$($ybus$($i$,$ j$))*$ sin$($theta$($i$)-$ theta$($j$)))$;

Q$\_$eq$($i$)=$ Q$\_$eq$($i$)+$ V$($i$)*$ V$($j$)*...$

$($real$($ybus$($i$,$ j$))*$ sin$($theta$($i$)-$ theta$($j$))-...$

imag$($ybus$($i$,$ j$))*$ cos$($theta$($i$)-$ theta$($j$)))$;

else

$\%$ Diagonal self$-$contribution

P$\_$eq$($i$)=$ P$\_$eq$($i$)+$ V$($i$)^2*$ real$($ybus$($i$,$ i$))$;

Q$\_$eq$($i$)=$ Q$\_$eq$($i$)-$ V$($i$)^2*$ imag$($ybus$($i$,$ i$))$;

end

end

end

$\%$ Simplify equations for better readability

P$\_$eq $=$ simplify$($P$\_$eq$)$;

Q$\_$eq $=$ simplify$($Q$\_$eq$)$;

end

function theta $=$ dc$\_$power$\_$flow$($ybus$)$

$\%$ Compute DC power flow solution $($angles only$)$

$\%$ Known values for power generation and loads

PG $=[0$; $0\mathrm{.}5$; $1\mathrm{.}0$; $0$; $0$; $0]$; $\%$ Real power generation at buses $1$ to $6$

PL $=[0$; $0\mathrm{.}2$; $0\mathrm{.}1$; $0\mathrm{.}5$; $0\mathrm{.}3$; $0\mathrm{.}2]$; $\%$ Real power load at buses $1$ to $6$

$\%$ Net power injections P $=$ PG $-$ PL

P $=$ PG $-$ PL;

P$(1)=0$; $\%$ Slack bus power set to $0$ for DC power flow

$\%$ Convert Ybus to susceptance matrix B $($ignore resistance$)$

B $=-$imag$($ybus$)$;

$\%$ Remove the slack bus $($assume bus $1$ as the slack bus$)$

B$\_$reduced $=$ B$(2$:end, $2$:end$)$;

P$\_$reduced $=$ P$(2$:end$)$;

$\%$ Solve for voltage angles theta $($excluding the slack bus$)$

theta$\_$reduced $=$ B$\_$reduced $\backslash$ P$\_$reduced;

$\%$ Append the slack bus angle $($theta$1=0)$

theta $=[0$; theta$\_$reduced$]$;

end