Question: Suppose the following data points are generated by a smooth function $f(x)$ : begin{tabular) (CCCCCCCC) Whline $mathrm{x}$ 80 & $1 / 3$ & $2 /

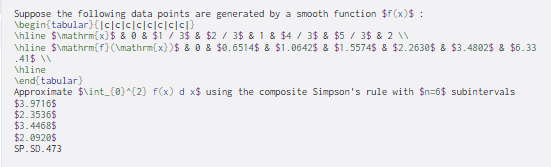
Suppose the following data points are generated by a smooth function

Suppose the following data points are generated by a smooth function $f(x)$ : \begin{tabular) (CCCCCCCC) Whline $\mathrm{x}$ 80 & $1 / 3$ & $2 / 3$ & 1 & $4 / 3$ & $5 / 3$ & 2 N Whline $\mathrm{f}\mathrm{x})$ & 0 & $0.6514$ & $1.0642$ & $1.55745 & $2.2630$ & $3.4862$ & $6.33 .41$ Whline \end{tabular Approximate $\int_{0}^{2} f(x) d x$ using the composite Simpson's rule with $n=5$ subintervals $3.97165 $2.3536$ $3.4468$ $2.09205 SP.SD.473

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Suppose the following data points are generated by a smooth function f (x): 1/3 2/3 1 4/3 5/3 2 f (x) 1.5403 0.9043 0.3092 0.0100 0.1347 0.6300 1.2837 The approximation of f(x) dx using the composite...

Suppose the following data points are generated by a smooth function $f(x)$ : \begin{tabular}{CCCCCCCC) Whline $\mathrm{x}$ & 5-15 & $-27 3$ & $-1 / 3$ & & & $1 / 3$ & $2 / 3$ & W Whline...

Suppose the following data points are generated by a smooth function $f(x) $ : \begin{tabular}| CICICCICICICCI Whline $\mathrm{x}$ 80 & $\pi / 65 & $\pi / 3$ & $\pi / 2$ & $2 \pi / 3$ & $5 \pi / 6$ &...

Suppose the following data points are generated by a smooth function $f(x)$: \begin{tabular ICICICICICICICCD) hline 5\mathrm{x} $ & 0& $\pi / 65 & $\pi / 35 & $\pi / 2$ & $2 \pi / 3$ & $5 \pi / 6$ &...

Suppose the following data points are generated by a smooth function $f(x)$ : \begin{tabularHICCICICICICICICL] Whline S\mathrm{x}$ & S-18 & $-27 3$ & $-1/3$ & & $1 / 3$ & $2 / 3$ & IN Whline...

Suppose the following data points are generated by a smooth function $f(x)$ : \begin tabular) ICICICICCICICC) Vhline \mathrm{x}$ 8 5-15 & 5-2 / 3$ & $-1/35 & 0 & $1 / 3$ & $2 / 35 & 1 W Xhline...

#1 STA355H1F due Wednesay, October 5, 2016 Problems to hand in: 1. Suppose that X1 , , Xn are independent Exponential random variables with density f (x; ) = exp(x) for x 0 where > 0 is an unknown...

MATLAB ASSIGN 1- Follow Directions and Complete. Will Thumbs Up! Directions: Unless otherwise specified, your write-up should contain the MATLAB input commands, the corresponding output, and the...

Math\t107-6381\t-\tQuiz\t#4\t-\tSchultz\t-\tDue\tFebruary\t21,\t2016\t-\tpage\t1\tof 3 Follow\tthese\tdirections\tcarefully. This\tquiz\tis\tdue\tby\t11:59\tEastern\ttime\ton\tFebruary\t21,\t2016. o...

(a) As the owner of a small architectural firm, you approach the Commonwealth Bank to obtain a term loan so that the firm can buy a new computer-aided drawing machine. The bank offers your company a...

Pang Corporation owns 80 percert interest in Sunda Corporation. On January 1, 2016, Sunda purchased S100,000 par of Pang's $1,000,000 outstanding bonds for S98,000 in the bond market. Pang's bonds...

Many physicians wait for weeks after an injury to initiate strengthening exercises because by then the new collagen is fairly mature and the risk of rupture lessens. 4 - 6 weeks 2 weeks 3 weeks 1 0...

Madison Corporation had the following common stock record during the current calendar year: Outstanding-January 1 2,090,000 Additional shares issued 3/31 109,000 Distributed a 10% stock dividend on...

5. Choose the appropriate evaluation design based on the characteristics of the company and the importance and purpose of the training.

8. One way to diagnose transfer of training problems or to ensure that transfer of training occurs is to complete the matrix shown below. This matrix considers the responsibilities of the manager,...

5. This assignment relates to Application Assignment 2 in Chapter 4. You now receive the following e-mail from the vice president of operations. Prepare an answer. Thanks for your recommendations...