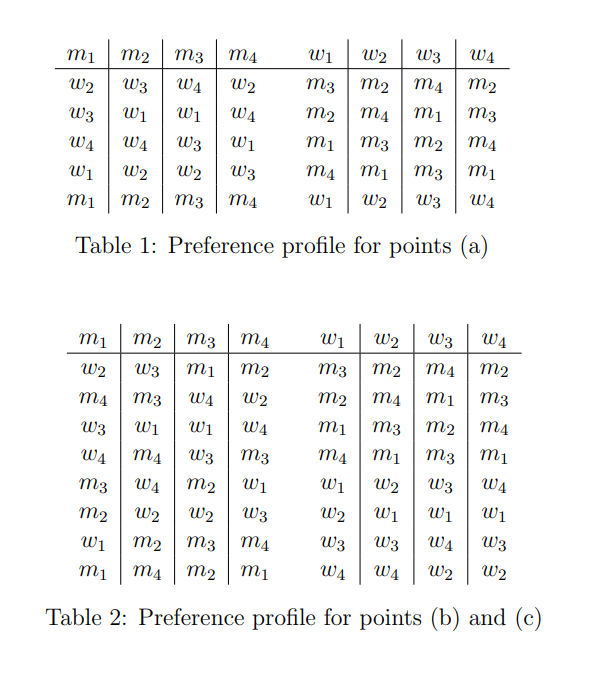
Suppose there are 4 men: M = {m1, m2, m3, am4} and 4 women W = {w1, w2, w3, w4} in a marriage market. Each man has a preference list over the women and each woman has a preference list over the men. Both are represented in table 1.

(a) Find the women-optimal stable matching in this problem and let's call it .

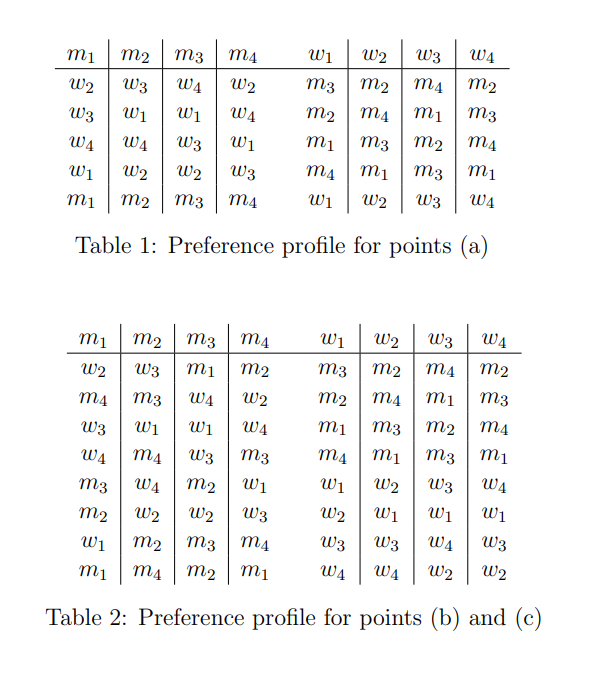
(b) Now consider that marriages are no more restricted between a man and a woman and let us add the new matching alternatives to the preferences of the agents in the table 2. Is still stable with respect to the expanded preferences? Motivate your answer.

(c) Is Pareto efficient with respect to the preferences stated in Table 2?